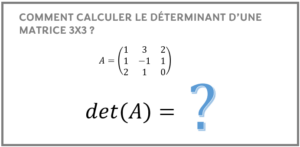L’objectif est d’apprendre à calculer le déterminant d’une matrice par la méthode d’expansion en cofacteurs avec des exercices résolus.
Sommaire
Rappel et mise en contexte du déterminant d’une matrice
Une matrice est un tableau carré ou rectangulaire dans lequel sont disposés des éléments. Une matrice peut donc avoir plusieurs lignes et plusieurs colonnes.
Si une matrice a autant de ligne que de colonne, alors on dit qu’on a une matrice carrée. Si le nombre de lignes est différent du nombre de colonnes, on dit qu’on a une matrice rectangulaire.
Le déterminant d’une matrice n’existe que pour les matrices carrées.
Le nombre de lignes et le nombre de colonnes d’une matrice constituent ce qu’on appelle la dimension d’une matrice ou la taille d’une matrice. On parle alors par exemple d’une matrice A de dimension (n x m) où n est le nombre de lignes et m est le nombre de colonnes.
Les éléments d’une matrice sont appelés les coefficients de la matrice. Un coefficient est caractérisé par le numéro de sa ligne et de sa colonne. Ainsi, on parle de coefficient aij où i est le numéro de la ligne et j le numéro de la colonne.
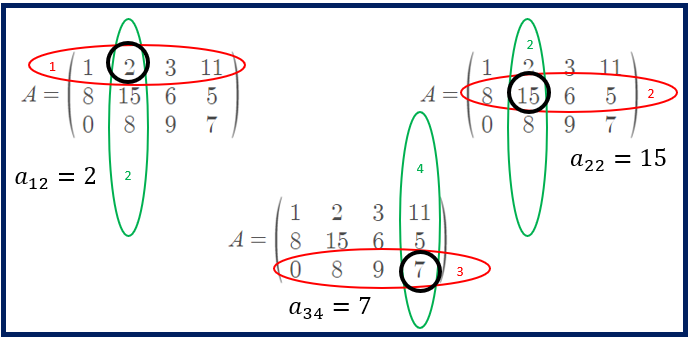
Savoir lire les coefficients d’une matrice est très important si on souhaite un jour savoir calculer le déterminant d’une matrice. Sur l’image, on peut voir par exemple que :
- Le chiffre 2 est le coefficient a12 (première ligne deuxième colonne). On note: a12=2.
- Le chiffre 15 est le coefficient a22 (deuxième ligne deuxième colonne). On note: a22=15.
- Le chiffre 7 est le coefficient a34 (troisième ligne quatrième colonne). On note: a34=7.
Calcul du déterminant d’une matrice 2×2
Définition
Une matrice carrée A c’est-à-dire une matrice A de dimension (n x n) admet une valeur (un chiffre) appelée déterminant de la matrice A ou tout simplement déterminant de A. On note det (A) ou |A|.
Les deux barres signifient déterminant. Regardons illustration suivante:
Illustration 1

Voyons maintenant comment se calcule le déterminant d’une matrice.
Déterminant d’une matrice 2X2
Nous commençons par le cas du plus simple pour le calcul du déterminant de matrice 2×2.
Le déterminant d’une matrice 2×2 est obtenu en effectuant le produit des éléments opposés et en calculant la différence entre ces produits. Il est plus facile de le comprendre par un schéma.
Illustration 2
Considérons l’illustration suivante:
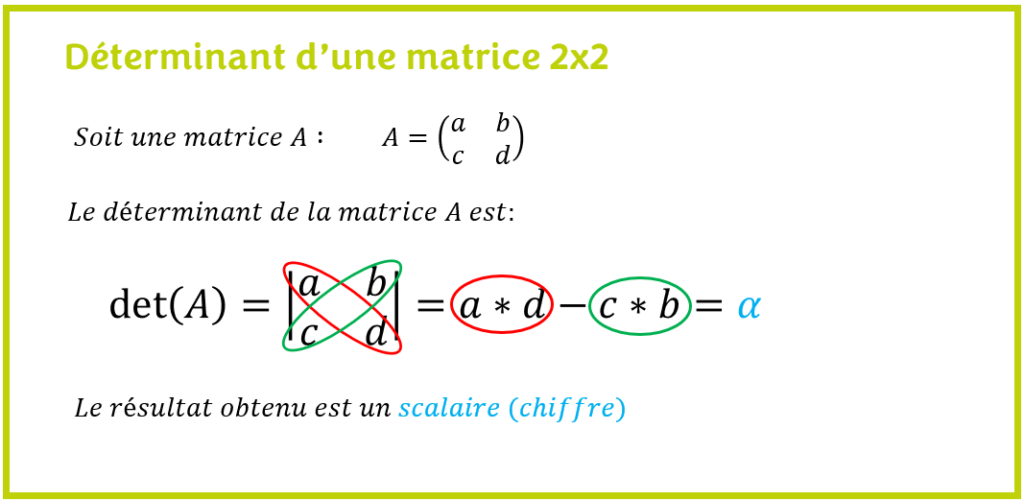
Le déterminant d’une matrice 2×2 est un produit croisé semblable à celui de l’égalité entre deux fractions auxquelles on fait une différence (mnémotechnique).
Voyons cela dans un exemple maintenant.
Exemple 1
Considérons l’exemple suivant:
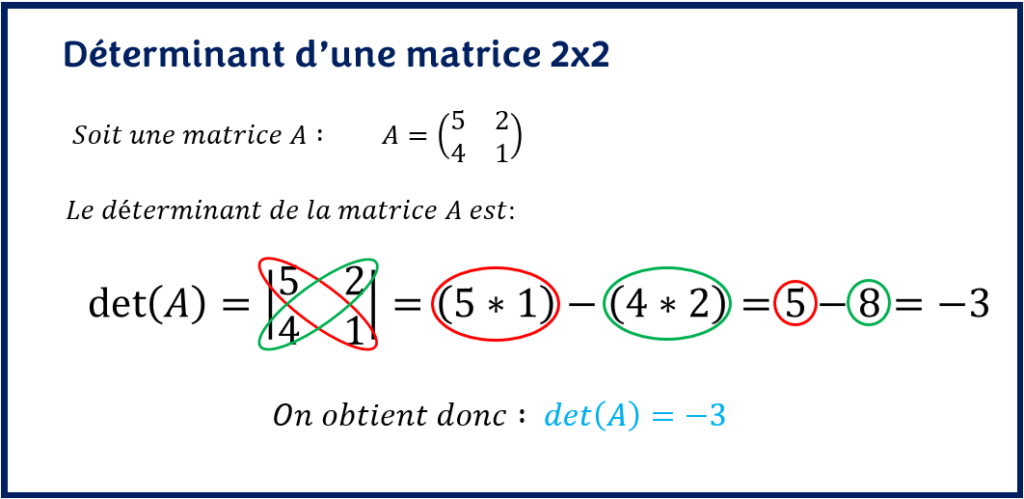
Ici, il faut faire très attention à l’ordre dans lequel on commence le produit croisé. En effet, commencer dans l’ordre inverse donnerait un résultat opposé.
Calcul du déterminant d’une matrice 3X3
Mineur d’une matrice
Un mineur se note Mij avec i le numéro de la ligne et j le numéro de la colonne.
Le mineur Mij est le déterminant de la matrice obtenu en éliminant la i-ème ligne de la j-ème colonne de la matrice.
Dans une matrice, on peut calculer plusieurs mineurs. Supposons une matrice A de dimension 3×3, alors on peut définir par exemple les mineurs M12 ou M22 .
Exemple 2
Considérons l’exemple suivant:

Un mineur est un déterminant. On le calcule en éliminant les lignes et les colonnes concernées. Ici, il est possible de calculer 9 mineurs (3 lignes*3 colonnes) correspondant à la dimension de la matrice :
- Mineur M11 : déterminant calculé en éliminant la première ligne et la première colonne de la matrice
- Mineur M12 : déterminant calculé en éliminant la première ligne et la deuxième colonne de la matrice
- Mineur M13 : déterminant calculé en éliminant la première ligne et la troisième colonne de la matrice
- Mineur M21: déterminant calculé en éliminant la deuxième ligne et la première colonne de la matrice
- Mineur M22 : déterminant calculé en éliminant la deuxième ligne et la deuxième colonne de la matrice
- Mineur M23 : déterminant calculé en éliminant la deuxième ligne et la troisième colonne de la matrice
- Mineur M31 : déterminant calculé en éliminant la troisième ligne et la première colonne de la matrice
- Mineur M32 : déterminant calculé en éliminant la troisième ligne et la deuxième colonne de la matrice
- Mineur M33 : déterminant calculé en éliminant la troisième ligne et la troisième colonne de la matrice
Cette notion sera très importante pour le calcul du déterminant ainsi que l’inverse des matrices 3×3.
Cofacteur d’une matrice
Le cofacteur se note Cij avec i le numéro de la ligne et j le numéro de la colonne.
Le cofacteur Cij se définit à partir du mineur Mij par la relation: Cij= (-1)i+jMij
À partir de la définition, on peut donc voir que le cofacteur et le mineur ont toujours la même valeur numérique en valeur absolue. Leurs signes diffèrent en fonction du numéro de la ligne et la colonne.
Regardons ceci dans un exemple
Exemple 3
Considérons l’exemple suivant :

En pratique, on n’utilise pas vraiment cette formule pour calculer le cofacteur. On s’intéresse surtout au calcul du mineur puis on le multiplie par le signe « – » (moins) au besoin en fonction du numéro de la ligne et de la colonne. Les signes du cofacteur pour une matrice sont déjà connus d’avance. Regardez l’illustration ci-dessous :
Signe des cofacteurs d’une matrice

Le signe des cofacteurs de la matrice s’obtient en mettant toujours le signe + (plus) sur l’élément de la première ligne et la première colonne, ensuite en déduisant les autres signes sur la matrice par alternance des signes.
Le cofacteur C23 a été calculé différemment de l’exemple précédent sans vraiment utiliser toute la formule. En fait, en pratique, on calcul le mineur ensuite on multiplie le résultat par le signe du cofacteur correspondant. Dans notre exemple, le signe du cofacteur était négatif (-).
Méthode d’expansion par cofacteur
Il existe plusieurs méthodes pour calculer le déterminant des matrices 3×3, nous allons présenter ici la méthode d’expansion par cofacteurs, car certaines notions n’ont pas encore été abordées.
Cette méthode est la plus répandue et la plus utilisée pour calculer le déterminant des matrices d’ordre plus grand.
Soit une matrice carrée A et Cij ses cofacteurs. Le déterminant de la matrice A est obtenu en suivant une expansion par cofacteurs dans le respect des règles suivantes:
- Choisir une ligne ou une colonne de la matrice A (prendre de préférence la ligne ou la colonne contenant le plus de zéros possible )
- Multiplier chacun des éléments ܽaij de la ligne (ou colonne) choisie par son cofacteur Cij correspondant
- Additionner chacun des résultats
Il existe donc plusieurs façons différentes de calculer le déterminant d’une matrice selon la ligne ou la colonne qu’on la calcule.
Par exemple, en choisissant une expansion selon la première ligne, le déterminant serait :
det (A)=a11C11+a12C12+a13C13
En choisissant une expansion selon la deuxième colonne, le déterminant serait:
det (A)=a12C12+a22C22+a32C32
Remarquez que lorsqu’on choisit la ligne ou la colonne pour le calcule du déterminant, l’indice reste celui-ci reste fixe.

Que l’on développe le calcul du déterminant selon une ligne ou une colonne, on trouve le même résultat pourvu que les calculs soient corrects.
Déterminant d’une matrice 3×3
En pratique, à l’étape 2 dans la méthode d’expansion par cofacteur, on marque le signe des cofacteurs au-dessus de chaque chiffre comme dans l’astuce présentée plus haut. Ensuite, on multiplie chaque mineur par le coefficient à l’intersection du mineur Mij de la ligne ou de la colonne correspondante choisi combiné au signe de son cofacteur. Enfin, on fait une somme algébrique de tous les résultats.
Nous allons clarifier ceci dans l’exemple ci-dessous:

On n’a pas besoin de retenir de formules pour le calcul du déterminant. Il faut juste se rappeler qu’on développe le calcul suivant la ligne ou la colonne contenant le plus de zéros. Dans notre exemple, on aurait aussi pu faire le calcul en utilisant la dernière ligne.
En partant de la colonne choisi, on multiplie les mineurs associés à chaque coefficient suivi du signe du cofacteur:
- +4 est le coefficient a11, donc on le multipliera par le mineur M11
- -3 est le coefficient a21, donc on le multipliera par le mineur M21
- +0 est le coefficient a31, donc on le multipliera par le mineur M31. Puisque le coefficient est nul, alors ce n’est pas la peine de calculer le mineur (tout nombre multiplié par zéro est égal à zéro). C’est justement la raison pour laquelle on développe le déterminant d’une matrice en utilisant la ligne ou la colonne avec le plus de zéros.
La somme de tous ces produits est le déterminant de la matrice A.
Déterminant d’une matrice 4X4
La méthode présentée dans le cas des matrices 3×3 est aussi valide pour les matrices de plus grandes dimensions. On peut tout aussi appliquer la méthode d’expansion par cofacteur, mais nous n’allons pas faire d’exemples pour cette méthode dans cette partie.
L’exemple présenté ici sera basé sur l’astuce d’utiliser les signes des cofacteurs, car elle est plus rapide et représente ce qu’on utilise en pratique dans les exercices.
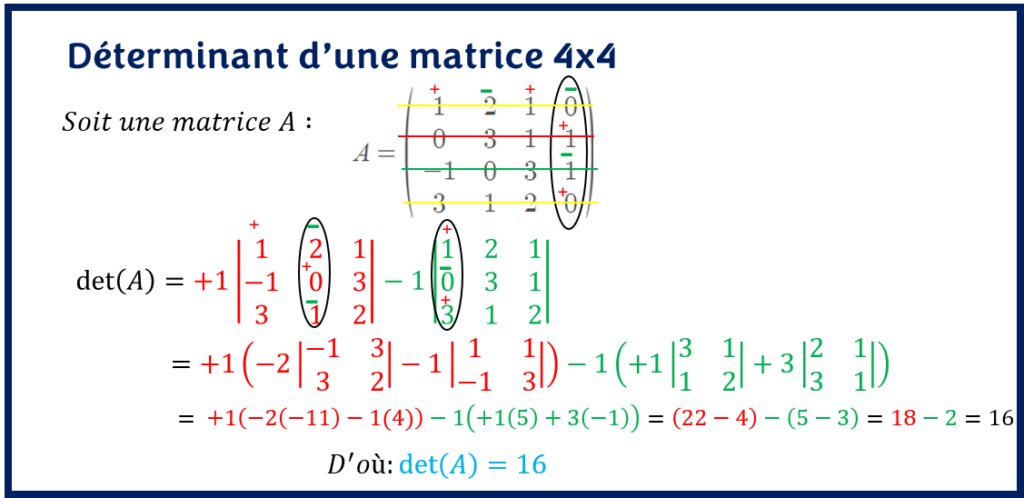
Vous remarquerez que les mineurs d’une matrice 4×4 sont des déterminants de matrice 3×3. Il faut être méthodique lorsqu’on calcule le déterminant de matrice d’ordre plus grand, car les risques d’erreurs sont plus grands. Il est important dans chaque étape de toujours choisir la ligne ou la colonne avec le plus de zéros possible pour faciliter les calculs.
Ici, vous remarquerez que les mineurs associés aux coefficients nuls n’ont pas été calculés.
Méthode de calcul du déterminant de dimension 3X3, 4X4, ou plus
- Choisir une ligne ou une colonne de la matrice A (prendre de préférence la ligne ou la colonne contenant le plus de zéros possible )
- Octroyer à chacun des éléments un signe +/- (signe des cofacteurs)en suivant la règle suivante : on associe un signe positif à la position ܽa11, puis on alterne les signes en se déplaçant horizontalement ou verticalement.
- Multiplier chacun des éléments aij(en considérant le signe des cofacteurs) de la ligne ou de la colonne choisie par son mineur correspondant c’est-à-dire le déterminant qu’il reste lorsqu’on élimine la ligne i et la colonne j dans lesquelles se trouve ܽle coefficient aij.
- Faire la somme algébrique de ces résultats afin de trouver le déterminant de la matrice.
Vous trouverez en vidéo comment trouver le déterminant d’une matrice 3×3.
Conseils et astuces
- Le déterminant d’une matrice est un scalaire (un chiffre). Il est nul si la matrice contient une ligne de zéro ou une colonne de zéro
- Pour les matrices rectangulaires, le déterminant n’existe pas. C’est une notion propre aux matrices carrées
- Vous pouvez utiliser cette plateforme pour effectuer vos opérations sur les matrices
FAQ sur le déterminant d’une matrice
Le déterminant d’une matrice 2×2 est obtenu en effectuant le produit des éléments opposés et en calculant la différence entre ces produits. Il est plus facile de le comprendre par un schéma. Pour les matrices 3×3, la méthode est différente.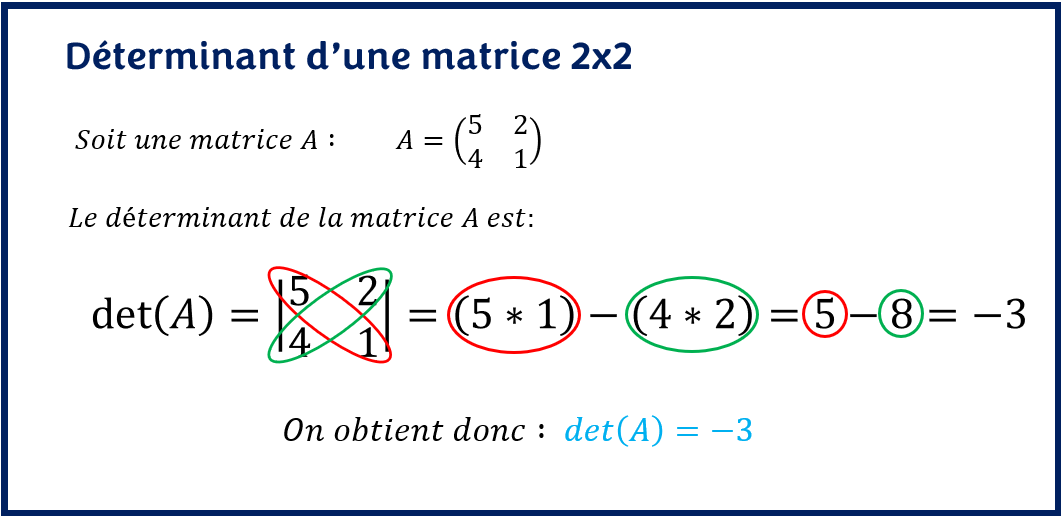
On marque le signe des cofacteurs au-dessus de chaque chiffre. Ensuite, on choisit la ligne ou la colonne contenant le plus de zéro puis, on multiplie chaque mineur Mij par le coefficient aij à l’intersection de la ligne ou de la colonne correspondante choisie combiné au signe de son cofacteur. Enfin, on fait une somme algébrique de tous les résultats.
On peut calculer le déterminant de matrice de dimension NxN en suivant la méthode suivante.
Quant aux matrices de dimension 2×2, il suffit de faire la différence des produits croisés de la matrice.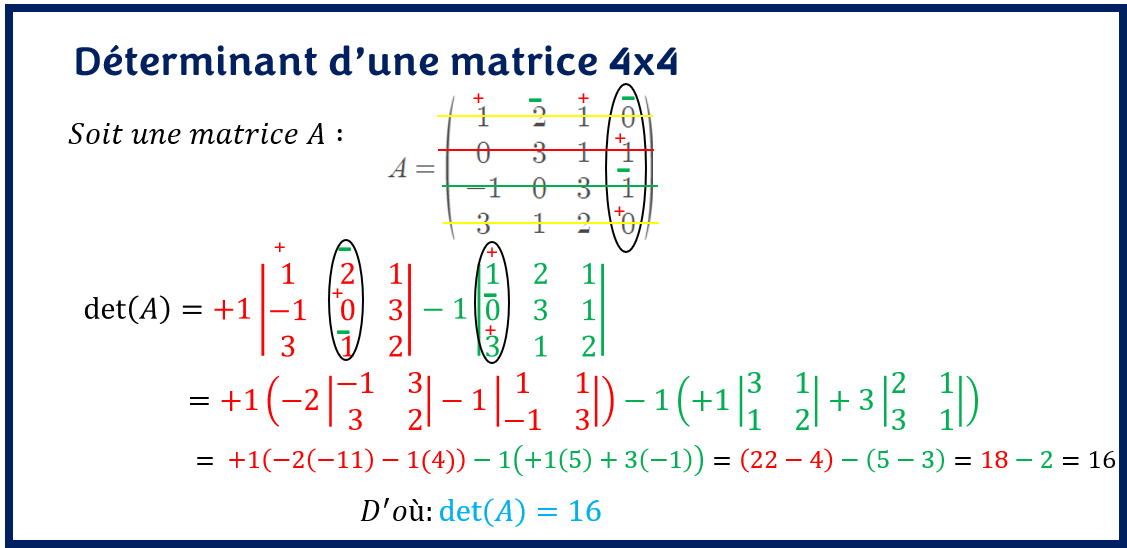
Le mineur Mij d’une matrice est le déterminant de la matrice obtenu en éliminant la i-ème ligne de la j-ème colonne de la matrice. 
Le cofacteur Cij se définit à partir du mineur Mij par la relation: Cij= (-1)i+jMij
À partir de la définition, on peut donc voir que le cofacteur et le mineur ont toujours la même valeur numérique en valeur absolue. Leurs signes diffèrent en fonction du numéro de la ligne et la colonne.
On ne peut pas calculer le déterminant d’une matrice rectangulaire (qui n’a pas le même nombre de lignes de colonne).
Sujets similaires
- PROPRIÉTÉS DU DÉTERMINANT D’UNE MATRICEL’objectif est d’apprendre à utiliser les propriétés du déterminant d’une matrice afin de calculer le déterminant sans calculer la matrice
- INVERSE D’UNE MATRICEL’objectif est d’apprendre à calculer l’inverse d’une matrice et de découvrir les propriétés de l’inverse avec des exemples résolus.
- COMMENT CALCULER LE DÉTERMINANT D’UNE MATRICE 3×3?Vous trouverez les étapes nécessaires et suffisantes sur comment calculer le déterminant d’une matrice 3×3 avec des exemples pratiques.
- DÉTERMINANT D’UNE MATRICEL’objectif est d’apprendre à calculer le déterminant d’une matrice par la méthode d’expansion en cofacteurs avec des exercices résolus.