L’objectif est d’apprendre à calculer l’aire d’un triangle et de connaître ses propriétés à partir d’exercices résolus.
Sommaire
Rappel et mise en contexte
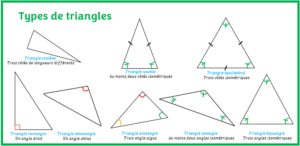
Un triangle est une figure géométrique comportant trois côtés, trois sommets et trois angles. C’est l’une des figures de base en géométrie qui possède de nombreuses propriétés intéressantes. Toutefois, il existe différents types de triangles classés en fonction de la longueur de leurs côtés (équilatéraux, isocèles ou scalènes) et de la mesure de leurs angles (aigus, droits, obtus).
Il est important de se familiariser à l’utilisation des triangles, car grâce à ses propriétés, ils sont utiles dans de nombreux problèmes en mathématiques, en géométrie, en trigonométrie et en ingénierie.
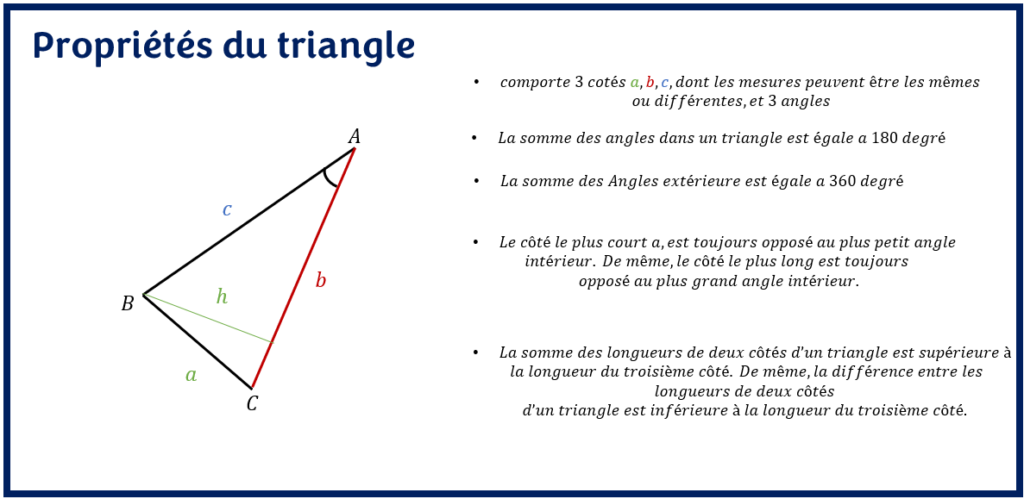
Le triangle se distingue d’autres figures géométriques par les propriétés suivantes:
- comporte 3 cotés et 3 angles dont les mesures peuvent être les mêmes ou différentes
- La somme des angles dans un triangle est égale à 180 degrés
- La somme des angles extérieure à un triangle est égale à 360 degrés
- Le côté le plus court est toujours opposé au plus petit angle intérieur. De même, le côté le plus long est toujours opposé au plus grand angle intérieur.
- La somme des longueurs de deux côtés d’un triangle est supérieure à la longueur du troisième côté. Il en est de même pour la différence entre les longueurs de deux côtés d’un triangle qui est toujours inférieure à la longueur du troisième côté.
- Les angles intérieurs et extérieurs consécutifs à un sommet d’un triangle sont supplémentaires.
Calcul de l’aire du triangle
Calcul de l’aire du triangle: Base et hauteur du triangle
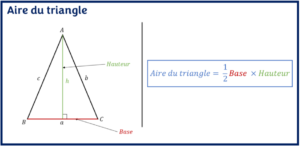
Dans un triangle, une hauteur est la droite perpendiculaire à un côté (appelé base) et passant par le sommet opposé à ce côté.
Tandis que, pour un triangle ayant un angle obtus(angle de plus de 90 degrés), la hauteur relative à la base contenant l’angle obtus du triangle se trouve à l’extérieur du triangle
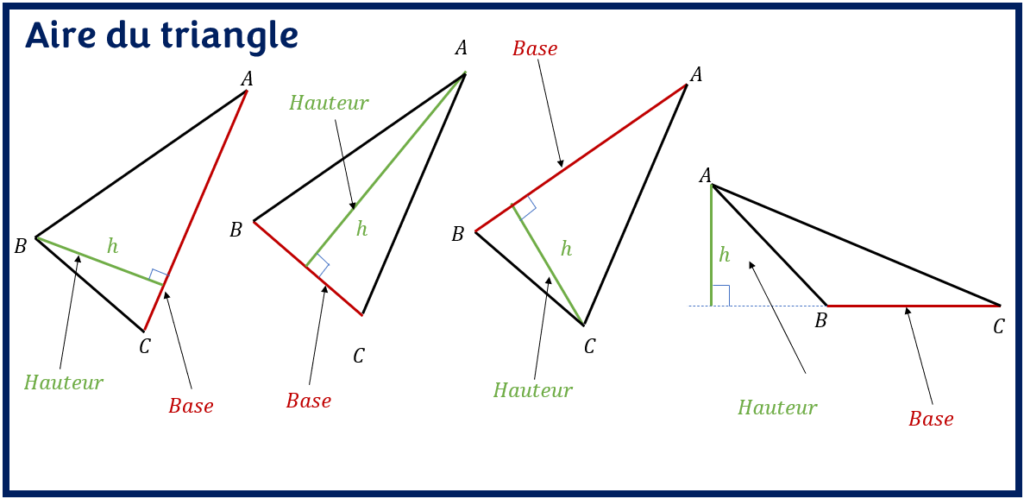
On voit bien que dans le dernier cas, la hauteur se trouve à l’extérieur du triangle. Ceci n’est pas faux puisque une hauteur n’est pas nécessairement à l’intérieur du triangle par définition.
Calcul de l’aire du triangle: Formule
Une fois que nous avons identifié la base et la hauteur du triangle, l’aire du triangle est égale à la moitié du produit de la hauteur et de la base du triangle. Il est donc une mesure de la surface interne du triangle. Toutefois, les deux autres côtés du triangle ne sont pas utilisés dans le cadre du calcul de la surface du triangle. Ces côtés pourront être utiles pour calculer d’autres mesures manquantes au besoin.
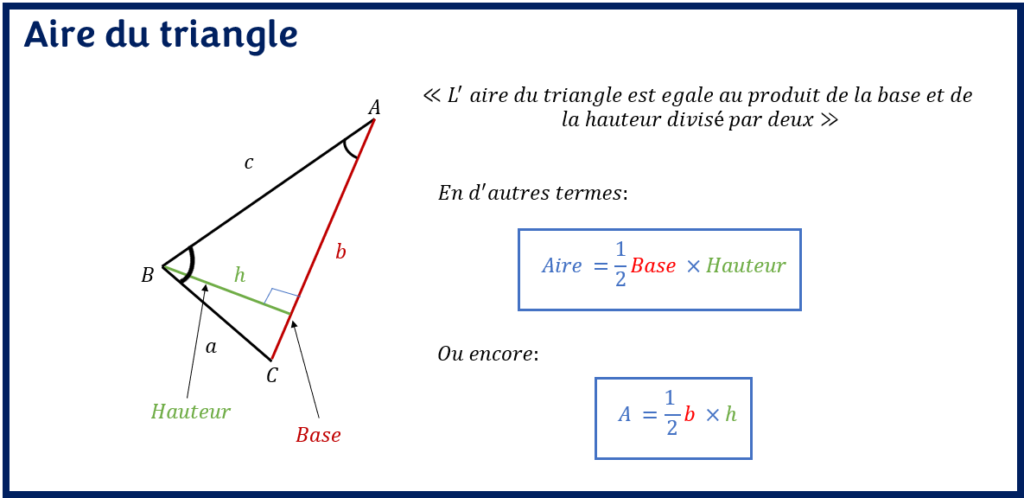
La formule de calcule de l’aire du triangle est le suivant:
A = (1/2) * Base * Hauteur
A = (1/2) * B * H
où, B est la base, H est la hauteur
Calcul de l’aire du triangle: Exemple
Le calcul de l’aire d’un triangle est assez simple si l’on connaît les mesures de la base et de la hauteur. Mais, dans la plupart des problèmes de calcul de surface, il sera nécessaire de calculer soi-même la mesure de la base ou de la hauteur du triangle avant de calculer son aire. Pour ce faire, vous disposez de plusieurs outils pour calculer ces mesures manquantes entre autres la relation de Pythagore, le théorème de Thalès, les rapports trigonométriques (SOH-CAH-TOA ou CAH-SOH-TOA), la loi des sinus et la loi des cosinus pour ne citer que cela.
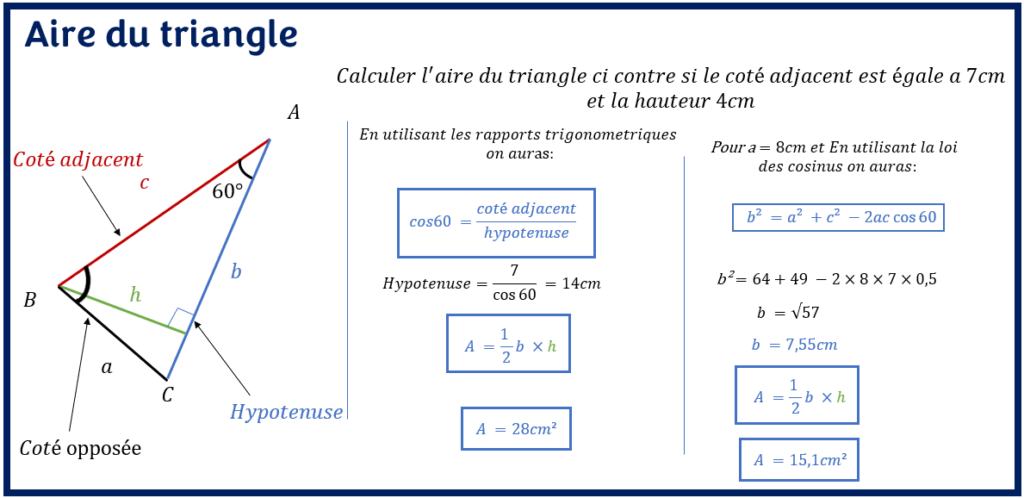
Calcul de l’aire du triangle: Formule de Heron
Dans un article précédent, nous avons vu comment calculer le périmètre d’un triangle. Maintenant, nous verrons ici comment calculer la surface du triangle connaissant son périmètre. Cette technique est appelée la formule de Héron. Elle est utilisée lorsque la mesure de la hauteur du triangle n’est pas donnée et que l’on connait toutes les autres mesures des côtés du triangle. La formule de base vue plus haut dans l’article ne peut s’appliquer directement sans effectuer au moins trois étapes intermédiaires. La formule de Heron est donc une alternative rapide et efficace pour ce type de problème.

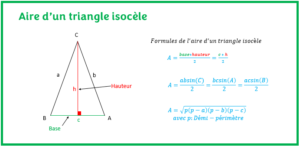
Tout d’abord, il est question de calculer le demi-périmètre (la moitié du périmètre) : s = (a+b+c)/2, où a,b,c sont les trois côtés d’un triangle. Maintenant, l’aire est donnée par :
A = √[s(s-a)(s-b)(s-c)]
Propriétés d’un triangle
Certaines propriétés communes d’un triangle incluent la somme de ses angles intérieurs étant de 180 degrés, en raison de la relation entre ses côtés et ses angles (comme le théorème de Pythagore pour les triangles rectangles) et les différents types de triangles (équilatéraux, isocèles, scalènes)
Conseils et astuces concernant l’aire d’un triangle
- Les triangles sont des figures géométriques
- La base et la hauteur du triangle se calculent en utilisant les relations trigonométriques ou le théorème de Pythagore
- Le côté le plus long du triangle est appelé hypoténuse
- Attention à la conversion d’unité lors du calcul de l’aire d’un triangle . La hauteur et la base doivent avoir la même unité.
- Consulter la vidéo explicative ou demander l’assistance d’un tuteur au besoin
Si vous n’avez toujours pas compris, vous pouvez consulter la foire aux questions .
FAQ sur l’aire d’un triangle
La formule de l’aire d’un triangle est A = (1/2)* base * hauteur 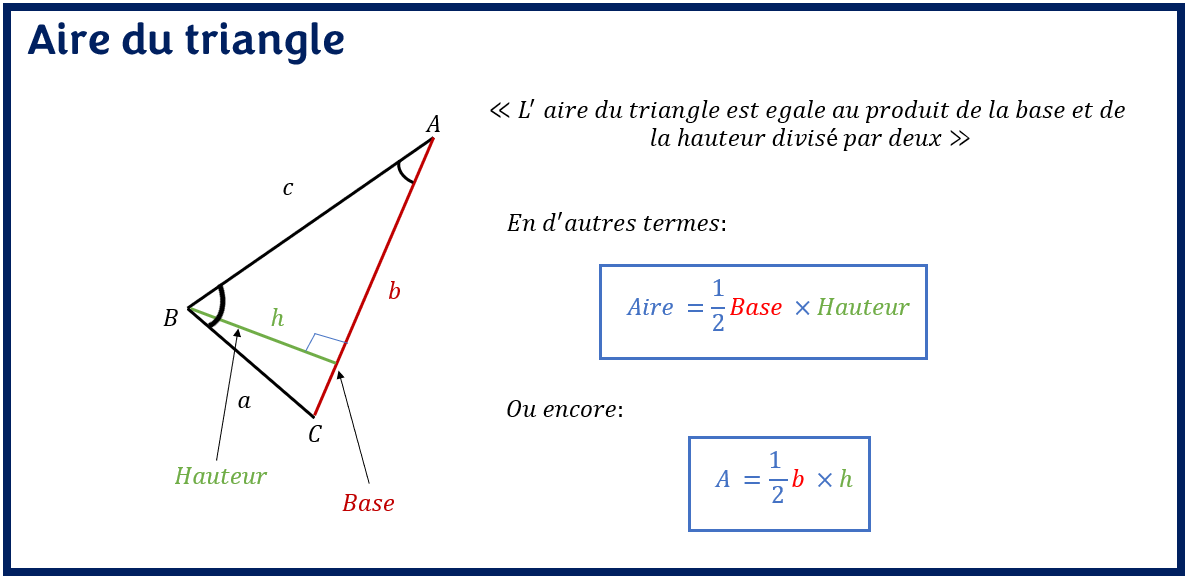
Il existe trois formules pour calculer l’aire d’un triangle. La première formule est d’utiliser la formule de base. La deuxième formule est d’utiliser la formule trigonométrique et la troisième forme est en utilisant la formule de Héron 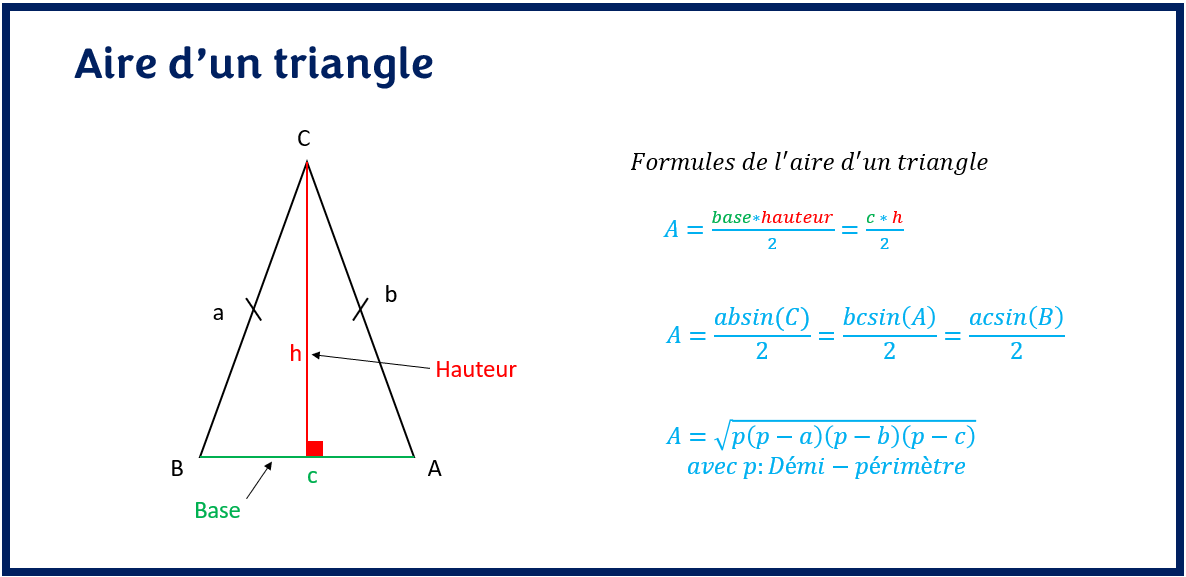
La hauteur d’un triangle est la distance perpendiculaire de la base au sommet opposé.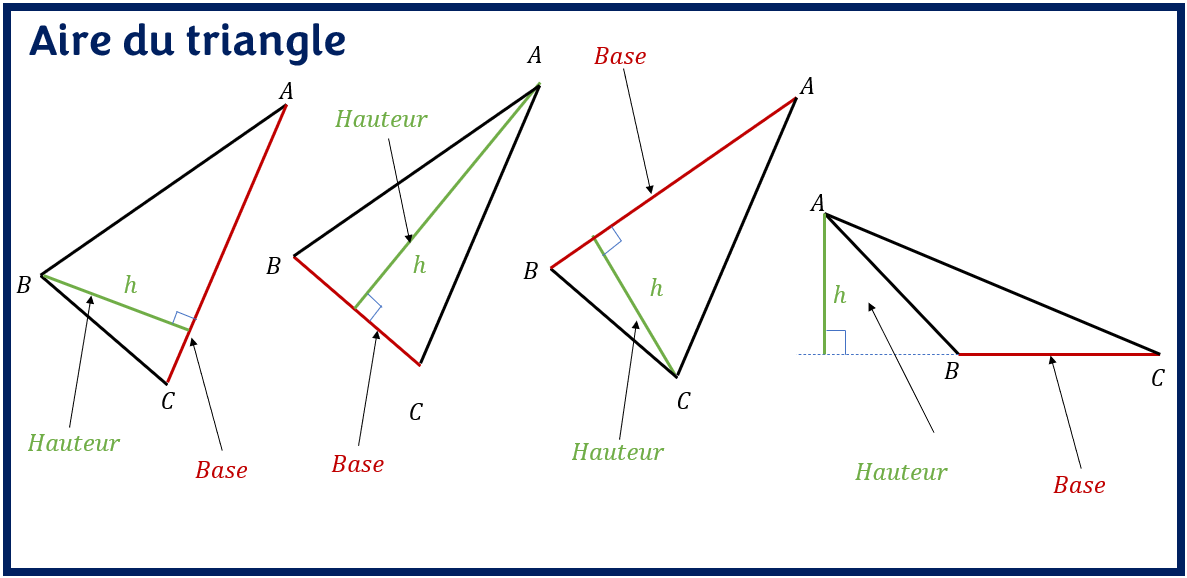
Sujets similaires
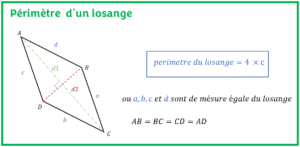
- Périmètre d’un losangeL’objectif est d’apprendre à calculer le périmètre d’un losange et de connaitre ses propriétés avec des exemples résolus.
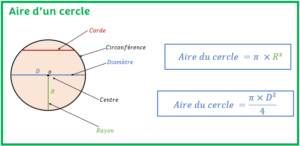
- Aire d’un cercleL’objectif est d’apprendre comment calculer l’aire d’un cercle et de connaitre ses propriétés avec des exemples résolus.
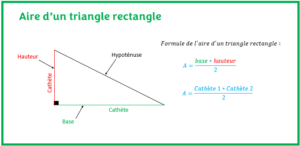
- Aire d’un triangle rectangleL’objectif est d’apprendre comment calculer l’aire d’un triangle rectangle de plusieurs façons différentes avec des exercices résolus.
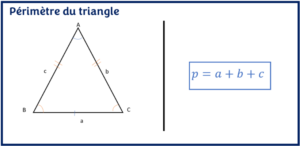
- Périmètre du triangleL’objectif est d’apprendre à calculer le périmètre du triangle et de connaître ses propriétés à partir d’exercices résolus.
- Aire du triangleL’objectif est d’apprendre à calculer l’aire d’un triangle et de connaître ses propriétés à partir d’exercices résolus.
- Aire d’un triangle isocèleL’objectif est d’apprendre à calculer l’aire d’un triangle isocèle de plusieurs façons différentes avec des exercices résolus.
- Les types de trianglesL’objectif est d’apprendre les différents types de triangles existants et leurs propriétés avec des exemples résolus.
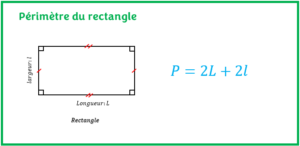
- Périmètre du rectangleL’objectif est d’apprendre à calculer le périmètre du rectangle et de connaître ses propriétés à partir d’exercices résolus.