LOI DES SINUS

L’objectif est d’apprendre à utiliser la loi des sinus dans un triangle afin de déterminer une mesure manquante dans un triangle quelconque.

Sommaire

Rappel et mise en contexte

Jusqu’ici, nous nous sommes principalement concentrés sur les relations mathématiques à l’intérieur d’un triangle rectangle. Nous avons vu plusieurs méthodes pouvant être utilisées pour déterminer des mesures manquantes dans ce type de triangle notamment: le théorème de Pythagore, les relations métriques et les rapports trigonométriques.

Maintenant, nous allons voir les relations mathématiques à utiliser lorsque le triangle n’est pas un triangle rectangle. À cet effet, citons entre autres la loi des sinus et la loi des cosinus.

Dans cet article, on parlera uniquement à loi des sinus. Pour cela, définissons le vocabulaire associé à ce concept.

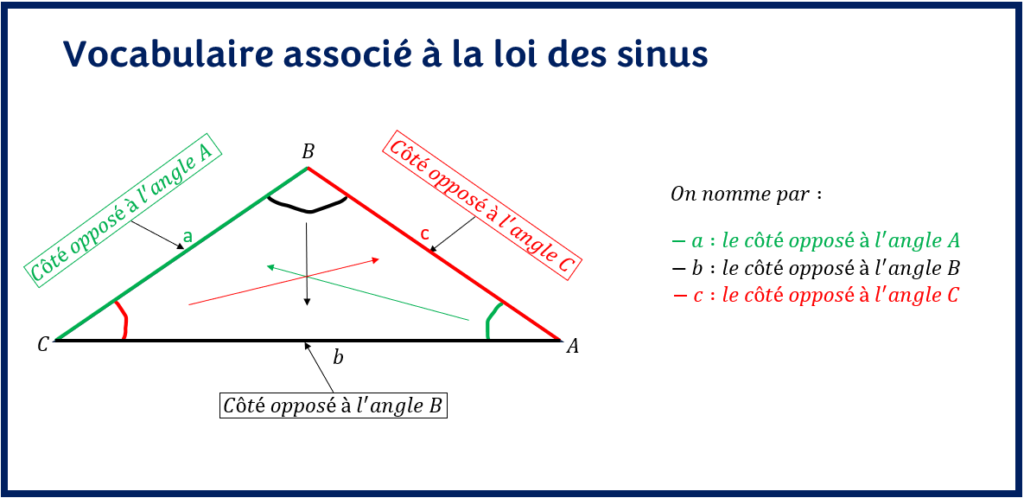
Le côté opposé à chaque angle est nommé par la lettre minuscule de son sommet opposé correspondant. À titre d’exemple, la lettre a correspond au côté opposé au sommet A ( donc à l’angle A) .

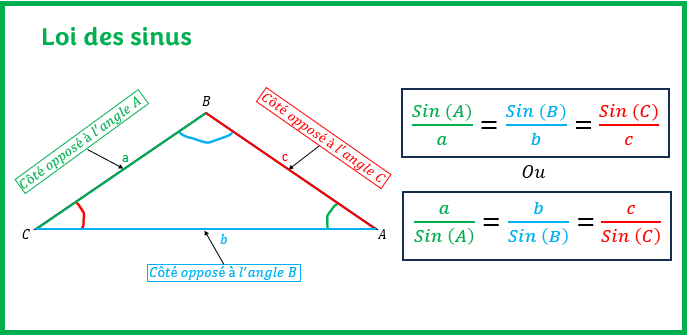
Loi des sinus

La loi des sinus s’énonce comme suit:

<< Dans un triangle quelconque ABC, les mesures des côtés sont proportionnelles au sinus des angles opposés à ces côtés >>

En d’autres termes, la loi des sinus s’écrit à partir de l’équation suivante:

sin(A)/a = sin(B)/b = sin(C)/c

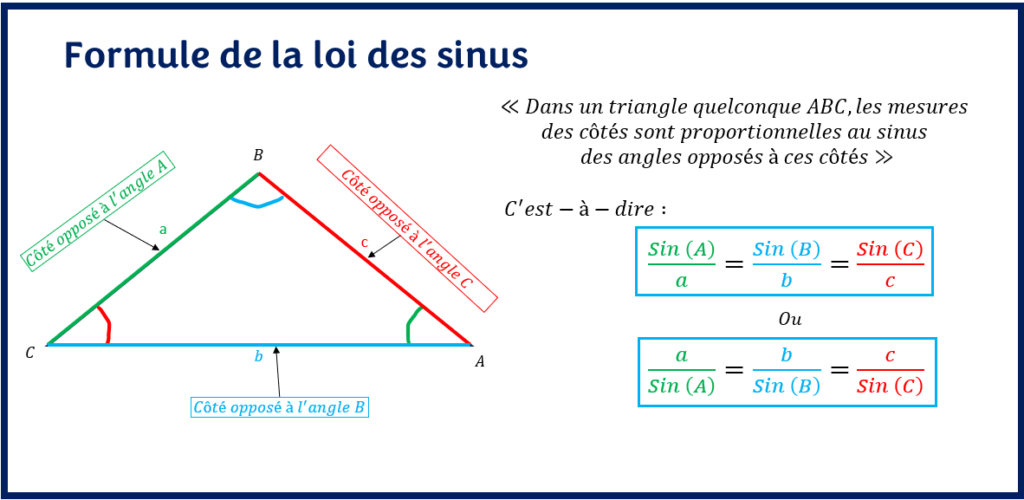
Étant donné que la loi des sinus est une relation de proportionnalité, les termes du numérateur et du dénominateur peuvent être permutés. L’important est donc de rester consistant dans le reste de la formule. Ainsi, on peut très bien également écrire les rapports suivants:

a/sin(A) = b/sin(B) = c/sin(C)

La relation des sinus s’utilise par paire de deux rapports au choix à sélectionner en fonction des données connues du problème.

Voyons maintenant comment nous pouvons calculer une mesure manquante avec la relation des sinus.

Calcul d’une mesure manquante dans un triangle quelconque avec la loi des sinus

Dans un triangle quelconque, la loi des sinus permet de trouver:

• La mesure d’un côté lorsque les mesures de deux angles et d’un côté sont connues
• La mesure d’un angle lorsque la mesure de son côté opposé, d’un angle et d’un autre côté du triangle est connue

Calcul d’une mesure manquante d’un côté du triangle avec la loi des sinus

Dans un triangle quelconque, la loi des sinus peut permettre de déterminer la mesure des côtés manquants. Pour cela, il est nécessaire de connaître les mesures de deux angles et la mesure d’un côté dans le triangle.

Pour déterminer une mesure manquante dans un triangle quelconque avec la loi des sinus, il faut suivre les étapes suivantes :

• Nommer les trois côtés du triangle par la lettre correspondante
  • Le côté opposé à chaque angle est nommé par la lettre minuscule de son sommet opposé correspondant
• Écrire la formule de la loi des sinus
• Cocher les données connues du problème et la mesure recherchée dans la formule
• Sélectionner la paire de rapports de proportionnalité à utiliser
  • Les deux rapports à utiliser sont ceux dont trois données sur quatre sont connues
• Isoler la mesure manquante en faisant le produit en croix (produit des extrêmes = produits des moyens)

Considérons les exemples suivants:

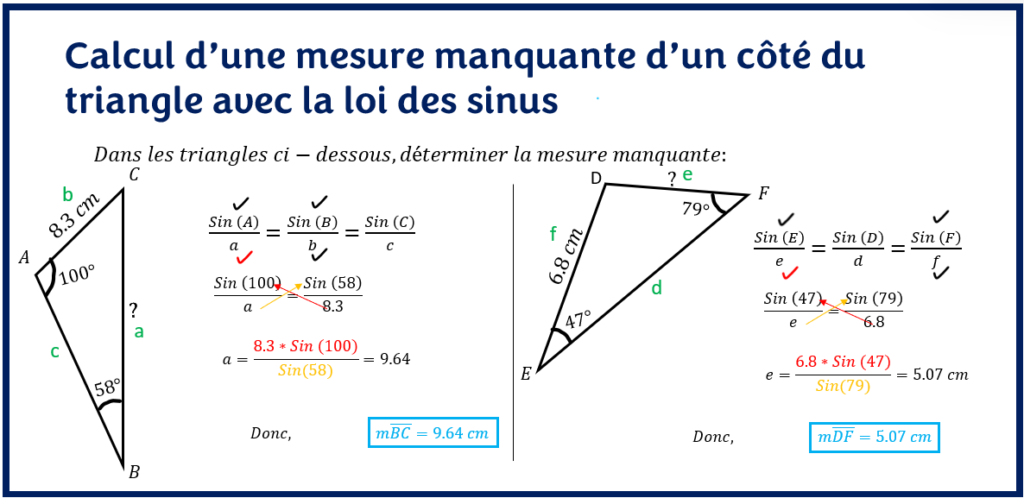
En suivant la méthodologie précédente, les côtés du triangle ont été renommés. À partir de la formule, on coche en noir les données connues du problème et en rouge la donnée inconnue. Par le produit en croix, on calcule la mesure du côté manquant.

Regardons maintenant comment calculer la mesure d’un angle manquant dans un triangle quelconque avec la relation des sinus.

Calcul d’une mesure manquante d’un angle du triangle avec la loi des sinus

Dans un triangle quelconque, la loi des sinus permet de déterminer la mesure d’un angle manquant. Pour cela, il est nécessaire de connaître les mesures de deux côtés du triangle et la mesure d’un angle dans ce triangle.

La méthodologie pour déterminer la mesure d’un angle manquant dans le triangle est la même que celle présentée ci-dessus.

Considérons les exemples suivants:

Le calcul d’un angle dans un triangle quelconque avec la relation des sinus présente certaines particularités au moment de donner le résultat final. La démarche de résolution est la même. Vous remarquez aussi que pour calculer l’angle, on utilise la fonction réciproque du sinus qui est sin^-1(x). Se référer au cours sur les rapports trigonométriques pour le calcul d’un angle manquant avec les rapports trigonométriques dans un triangle rectangle.

Aussi, deux angles supplémentaires ont le même sinus. Lorsqu’on calcule sin^-1 d’une valeur sur la calculatrice pour trouver un angle, le résultat donné par la calculatrice sera toujours un angle aigu(< 90°). C’est donc à nous de la corriger au besoin si on cherche un angle obtus, en calculant plutôt:

angle (obtus) cherché = 180° – angle (aigu) obtenu par la calculatrice

Observez à nouveau les deux exemples précédents. Dans le premier cas, l’angle ACB recherché est un angle aigu(< 90°), il n’y a donc pas de changement à faire puisque la valeur de l’angle donné par la calculatrice correspond déjà à un angle aigu.

Dans le deuxième cas, l’angle DEF recherché est un angle obtus (< 90°), le résultat final doit donc être modifié puisque la calculatrice nous retourne un angle aigu. On prend comme résultat : 180° – la valeur obtenue.

La loi des sinus est pour un triangle quelconque ce que sont les rapports trigonométriques pour le triangle rectangle. Pensez s’y!

Conseils et astuces sur la loi des sinus

• La loi des sinus s’utilise dans un triangle quelconque
• Elle permet de calculer la mesure d’un côté manquant. Il est nécessaire de connaître les mesures de deux angles et la mesure d’un côté dans le triangle.
• Elle permet de calculer la mesure d’un angle manquant. Il est nécessaire de connaître les mesures de deux côtés du triangle et la mesure d’un angle dans ce triangle.
• Le calcul de l’angle en utilisant la relation des sinus demande à réfléchir sur la nature de l’angle recherché: aigu(< 90°) ou obtus(> 90°)
• Le calcul de l’angle avec la calculatrice donnera toujours un angle aigu(< 90°)
• Si l’on cherche un angle obtus à partir de la relation des sinus, on doit trouver l’angle aigu correspondant puis calculer l’angle obtus recherché
• La relation des sinus peut s’appliquer aussi dans un triangle rectangle, mais il est préférable d’utiliser les rapports trigonométriques en utilisant les mnémotechniques SOH-CAH-TOA ou CAH-SOH-TOA.
• Dans un triangle, la somme des angles est de 180°. Si l’on connaît la mesure de deux angles, l’on peut calculer le troisième angle.
• Souvent, il est nécessaire d’effectuer la relation des sinus deux fois dans le même triangle pour calculer la mesure manquante recherchée.
• Il est souvent nécessaire de combiner la loi des sinus et la loi des cosinus pour résoudre un problème
• Si à la fin de la lecture de cours, vous ne comprenez toujours pas, vous pouvez soit consulter la vidéo explicative soit demander l’assistance d’un tuteur.

Vidéo explicative sur la loi des sinus

Vous pouvez consulter cette vidéo afin de mieux comprendre comment utiliser la loi des sinus.

Si vous avez toujours des questions, consultez la foire aux questions ci-dessous.

FAQ sur la loi des sinus

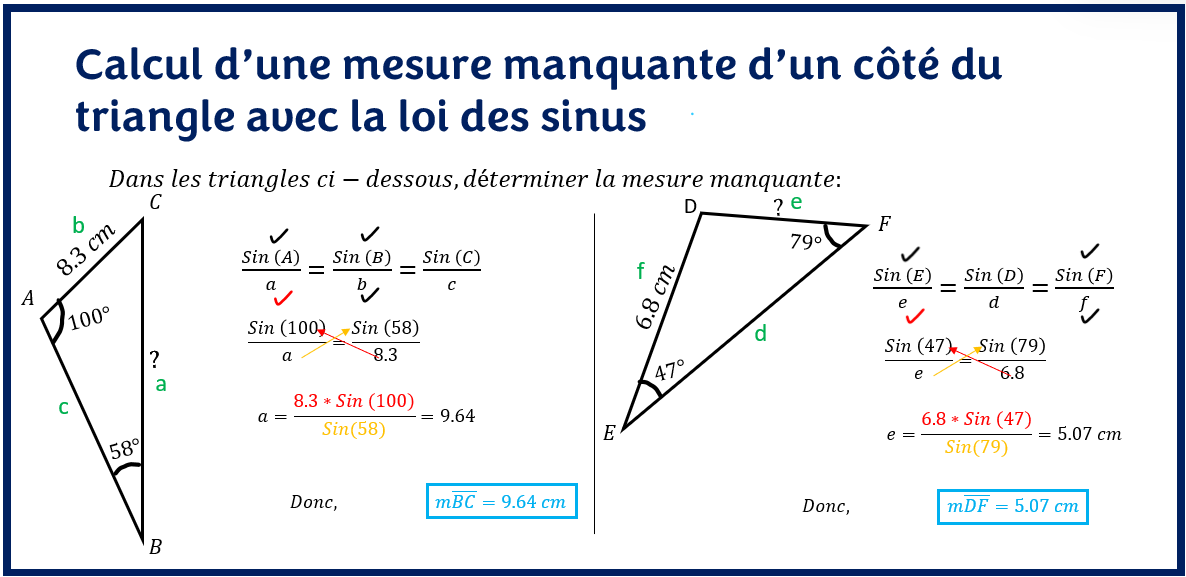
Sujets similaires

• 
  Périmètre d’un losange
  L’objectif est d’apprendre à calculer le périmètre d’un losange et de connaitre ses propriétés avec des exemples résolus.
• 
  Aire d’un cercle
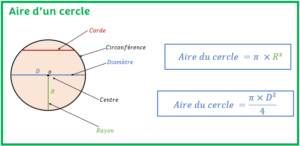  L’objectif est d’apprendre comment calculer l’aire d’un cercle et de connaitre ses propriétés avec des exemples résolus.
• 
  Aire d’un triangle rectangle
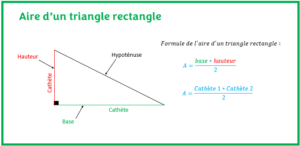  L’objectif est d’apprendre comment calculer l’aire d’un triangle rectangle de plusieurs façons différentes avec des exercices résolus.
• 
  Périmètre du triangle
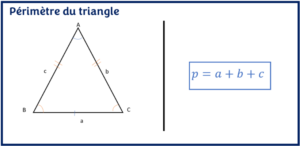  L’objectif est d’apprendre à calculer le périmètre du triangle et de connaître ses propriétés à partir d’exercices résolus.
• 
  Aire du triangle
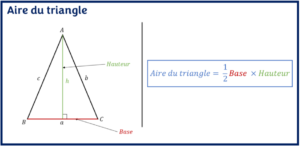  L’objectif est d’apprendre à calculer l’aire d’un triangle et de connaître ses propriétés à partir d’exercices résolus.
• 
  Aire d’un triangle isocèle
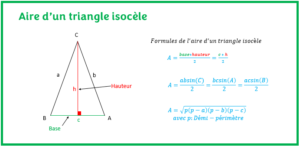  L’objectif est d’apprendre à calculer l’aire d’un triangle isocèle de plusieurs façons différentes avec des exercices résolus.
• 
  Les types de triangles
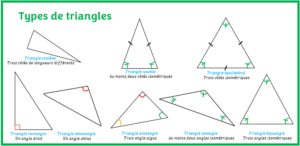  L’objectif est d’apprendre les différents types de triangles existants et leurs propriétés avec des exemples résolus.
• 
  Périmètre du rectangle
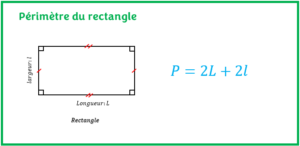  L’objectif est d’apprendre à calculer le périmètre du rectangle et de connaître ses propriétés à partir d’exercices résolus.
• 
  LOI DES COSINUS
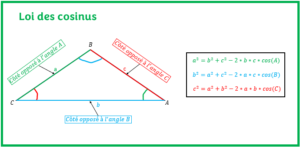  L’objectif est d’apprendre à utiliser la loi des cosinus dans un triangle afin de déterminer une mesure manquante d’un côté ou d’un angle dans un triangle quelconque.
• 
  LOI DES SINUS
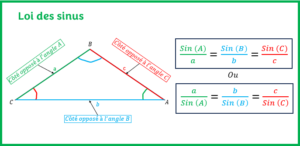  L’objectif est d’apprendre à utiliser la loi des sinus dans un triangle afin de déterminer une mesure manquante dans un triangle quelconque.
• 
  RAPPORTS TRIGONOMÉTRIQUES
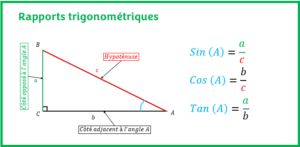  L’objectif ici est d’apprendre à utiliser les rapports trigonométriques pour calculer une mesure manquante ou un angle manquant dans un triangle rectangle avec des exemples résolus.
• 
  RELATIONS MÉTRIQUES DANS UN TRIANGLE RECTANGLE
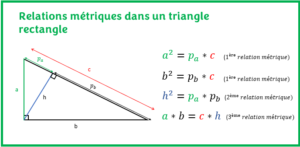  L’objectif est d’apprendre à utiliser les relations métriques dans un triangle rectangle pour déterminer une mesure manquante à partir d’exercices résolus.