L’objectif est d’apprendre à reconnaître et déterminer l’ensemble de solutions des équations linéaires avec des exemples résolus.
Sommaire
Rappel et mise en contexte
Les équations linéaires se rencontrent dans la grande majorité des exercices en algèbre linéaire. Il est donc important de savoir les reconnaître et de déterminer leur ensemble de solutions.
Nous avons déjà rencontré des équations linéaires à une seule variable au secondaire. Entre-temps, nous verrons le concept plus général des équations linéaires avec plusieurs variables.
Définition d’une équation linéaire
Une équation linéaire est une équation où tous les termes ne contiennent que des variables de degré 1.
Toute équation linéaire est une équation de premier degré qui peut s’écrire sous la forme a1x1+a2x2+a3x3+ …+ anxn=b. où x1, x2,…,xn sont les variables et les a1,a2,…,an sont les coefficients constants respectifs. b est aussi constant.

Exemples d’équations linéaires
Pour prendre un autre exemple, identifiez celles qui sont des équations linéaires. Justifiez vos réponses lorsqu’elles ne le sont pas.

Une équation qui n’est pas linéaire est dite non linéaire. Les équations non linéaires peuvent être reconnues lorsqu’on observe des termes suivant:
- les variables de degré n supérieur à 1(n positif)( xn)
- les fonctions trigonométriques(cos x, sin x, tan x, sec x, cotan x, cosec x),
- les racines n-ièmes(n√x),
- les produits de variables (xy, xz,yz,xyz, etc),
- les variables avec des exposants négatifs (n positifs)(x-n, 1/xn),
- les fonctions exponentielles(ex,exy, etc)
- les fonctions logarithmiques(ln x, log x, log xy, etc.).
Solution d’équations linéaires
Une solution d’une équation linéaire est un ensemble ou série de nombres qui permettent de vérifier l’équation linéaire. C’est-à-dire que si l’on remplace les variables de l’équation linéaire par la série de nombres, alors l’équation linéaire serait vraie.
Une solution d’une équation linéaire est appelée solution particulière.

Trouver une solution d’une équation linéaire consiste à trouver par essai-erreur des valeurs pour les inconnues qui rendent l’équation vraie. C’est ce que l’on appelle solution particulière.
Dans la prochaine partie, nous allons voir comment trouver systématiquement toutes les solutions d’une équation linéaire : c’est l’ensemble de solutions.
Ensemble de solutions des équations linéaires
L’ensemble de solutions d’une équation linéaire est l’ensemble de toutes les solutions possibles faisant en sorte que l’équation soit vraie. Cet ensemble de solutions se note: E.-S.
Résoudre une équation linéaire consiste à déterminer son ensemble de solutions. Cela dit, les étapes suivantes doivent être respectées:
- Isoler l’une des variables de l’équation linéaire afin de l’écrire en fonction des autres variables
- Poser les variables du membre de gauche comme des paramètres: ce sont des variables libres.
- Écrire l’ensemble de solutions de l’équation linéaire comme un couple de coordonnées formé par les variables de l’équation.

Une variable est dite libre si elle peut prendre n’importe quelle valeur. Un paramètre est une variable libre. L’ensemble de solutions d’une équation linéaire consiste donc à écrire les variables en fonction d’un ou de plusieurs paramètres.
Dans l’équation 1, si on pose t = 0, on obtient bien la solution particulière (3,0). En posant t = -1, on obtient bien une autre solution particulière (1,-1). On constate donc que pour chaque valeur du paramètre t qu’on choisit, on obtient une nouvelle solution à l’équation linéaire. On dit donc qu’on a une infinité de solutions.
Dans l’équation 2, on obtient également une solution à l’équation linéaire à chaque valeur des deux paramètres t et s. Si on prend par exemple, t = 2 et s = 2, on obtient la solution particulière (1,2,2).
Conseils et astuces sur les équations linéaires
- Une équation linéaire ne possède pas de variable avec un exposant plus grand que 1.
- Une équation linéaire ne possède pas de variable avec un exposant négatif.
- Une équation linéaire ne possède pas de termes avec les fonctions trigonométriques(sin(x), cos(x), tan(x)) , les fonctions exponentielles(ex) ou logarithmiques(ln x, log x).
- L’ensemble de solutions d’une équation linéaire s’écrit toujours en fonction d’un ou des paramètres.
- Un système d’équations linéaires est un ensemble de plusieurs équations linéaires.
- Pour vérifier qu’un couple de nombre est une solution d’une équation linéaire, il est question de vérifier que l’équation est vraie, en les substituant dans l’équation.
FAQ sur les équations linéaires
Une équation linéaire est une équation où tous les termes de l’équation sont de degré à 1 ou 0. Une équation non linéaire est une équation qui possède des termes non linéaires, notamment des variables de degré plus grand que 1, des fonctions trigonométriques, des fonctions de racines n-ièmes, des fonctions exponentielles ou logarithmiques.
Pour résoudre une équation linéaire, il faut:
– Isoler l’une des variables ou inconnues de l’équation linéaire afin de l’écrire en fonction des autres variables
– Poser les variables du membre de gauche comme des paramètres
– Écrire l’ensemble de solutions de l’équation linéaire comme un couple de coordonnées formé par les variables de l’équation.
Pour trouver l’ensemble de solutions d’une équation linéaire, il faut d’abord écrire l’une des variables en fonction des autres. Ensuite, il faut poser les variables du membre de gauche comme des paramètres et enfin écrire l’ensemble de solutions comme un couple de nombres en remplaçant chacune des variables par leurs expressions en fonction des paramètres.
Les équations linéaires à coefficients réels et constants sont les équations les plus simples à la fois à résoudre et à exprimer. Elles sont celles qu’on rencontre dans notre vie quotidienne comme lorsqu’on cherche à savoir si l’on aura assez d’argent pour faire nos courses à l’épicerie. Elles sont donc d’un grand intérêt pour l’apprentissage des mathématiques et servent de bases pour la résolution des systèmes d’équations linéaires plus complexes.
Une équation est dite linéaire si elle peut s’écrire sous la forme: a1x1+a2x2+a3x3+ …+ anxn=b. où les x1, x2,…,xn sont les variables et les a1,a2,…,an sont les coefficients respectifs. b est un coefficient constant.
Un autre point de vue serait qu’une équation est linéaire si elle ne contient pas de termes non linéaires(fonctions polynomiales de degré supérieur à 1, des fonctions trigonométriques, des fonctions de racine n-ièmes, des fonctions exponentielles ou logarithmiques à moins que ceux-ci soient constant.
Une équation non linéaire est toute équation qui n’est pas linéaire. C’est une équation qui contient au moins un terme non linéaire c’est-à-dire des fonctions polynomiales de degré supérieur à 1, des fonctions trigonométriques, des fonctions de racine n-ièmes, des fonctions exponentielles ou logarithmiques.
Une équation linéaire est une équation qui peut s’écrire sous la forme: a1x1+a2x2+a3x3+ …+ anxn=b. où les x1, x2,…,xn sont les variables et les a1,a2,…,an sont les coefficients respectifs. b est un coefficient constant.
Sujets similaires
Vous pouvez aussi consulter les articles suivants:
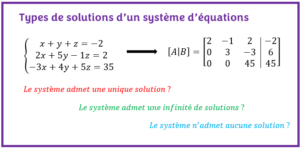
- COMMENT SAVOIR SI UN SYSTÈME ADMET UNE SOLUTIONDécouvrez les trois types de solutions d’un système. Apprenez comment savoir si un système admet des solutions avec des exercices résolus.
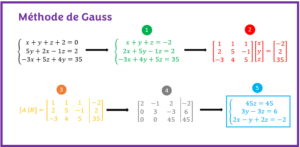
- MÉTHODE DE GAUSSL’objectif est d’apprendre à résoudre un système d’équations linéaires par la méthode de Gauss à partir d’exercices résolus.
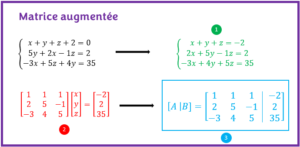
- MATRICE AUGMENTÉEL’objectif est d’apprendre à écrire la matrice augmentée d’un système d’équations et de l’échelonner à l’aide d’exercices résolus.
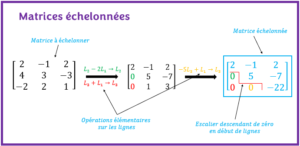
- MATRICES ÉCHELONNÉESL’objectif est d’apprendre à échelonner une matrice et à reconnaître les matrices échelonnées à l’aide d’exercices résolus.