MÉTHODE DE GAUSS

Jusqu’ici nous avons vu plusieurs méthodes pour résoudre un système d’équations linéaires. La méthode de comparaison, la méthode de substitution et la méthode par élimination sont des méthodes basiques vues au secondaire. Les méthodes plus avancées de résolution des systèmes d’équations linéaires sont la méthode de Gauss et la méthode de la matrice inverse.

La méthode de Gauss exige d’avoir une bonne base sur les matrices et la connaissance de notions préalable à savoir : la transformation d’un système sous la forme AX=B, la construction de la matrice augmentée d’un système et la connaissance des matrices échelonnées. Toutes ces notions ont déjà fait l’objet des articles précédents.

Résolution d’un système d’équations linéaires par la méthode de Gauss

Principe de la méthode de Gauss

La méthode de Gauss pour résoudre un système d’équations linéaires consiste à transformer la matrice augmentée correspondante au système d’équations en une matrice échelonnée.

En d’autres mots, la méthode de Gauss consiste à résoudre le système d’équations linéaires équivalents. Dans ce cas, il suffit de le résoudre le système du bas vers le haut. En commençant par la dernière équation et en utilisant les valeurs des inconnues précédentes dans les équations situées au-dessus.

La technique qui consiste à résoudre le système du bas vers le haut s’appelle la substitution inverse. Remarquez que c’est exactement la même méthode que la méthode de substitution que nous avons vus dans les articles précédents.

Étapes de résolutions d’un système d’équations par la méthode de Gauss

Pour résoudre un système d’équations linéaires par la méthode de Gauss, il faut suivre les étapes suivantes:

Réorganiser les équations du système pour avoir le même ordre d’apparition des variables dans chaque équations
Transformer le système d’équations sous la forme AX=B
Écrire la matrice augmentée [A|B] du système
Obtenir la matrice augmentée échelonnée
Résoudre le nouveau système d’équations du bas vers le haut à partir de la dernière équation

Étapes de résolutions d'un système d'équations par la méthode de Gauss

Opérations élémentaires autorisées dans la méthode de Gauss

Seulement trois opérations sont autorisées pour résoudre un système d’équations par la méthode de Gauss. Ces opérations sont :

permuter des lignes( L_i ↔ L_j ), c’est-à-dire ( L_i → L_j ) et ( L_j → L_i ).
Multiplier une ligne par une constante k, où k ∈ ℝ et k ≠ 0
Additionner un multiple k, où k ∈ ℝ, d’une ligne à une autre ligne ( L_i + kL_j→ L_i )

On peut également combiner ces opérations en une seule étape. Par exemple, en effectuant les opérations 2) et 3) précédentes simultanément sur les lignes L_i et L_j, nous obtenons k₁L_i + k₂L_j → L_i, où k₁ ≠ 0.

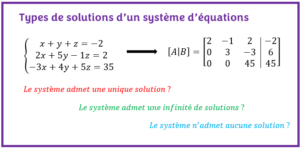
Types de solutions d’un système d’équation par la méthode de Gauss

Lorsqu’on résous un système d’équations linéaires par la méthode de Gauss, trois issues sont possibles :

le système possède une solution unique : un seule couple de nombre vérifient simultanément les égalités du système.
le système possède une infinité de solutions : plusieurs couples de nombre vérifient simultanément les égalités du système.
le système ne possède aucune solution : Aucun couple de nombre ne vérifient simultanément les égalités du système.

Le système possède une solution unique

Soit un système d’équations sous la forme AX=B. Le système d’équations possède une solution unique si:

le déterminant de la matrice A est différent de 0
la matrice échelonnée de la matrice A a un pivot sur chaque ligne
le rang de la matrice A est égale à son nombre de ligne
le rang de la matrice augmentée [A|B] est égale à son nombre de ligne
la matrice A est inversible
les colonnes de la matrice A sont linéairement indépendantes
les lignes de la matrice A sont linéairement indépendantes
le noyau de la matrice A est l’ensemble vide (Niveau universitaire)

Le système possède une infinité de solutions

Soit un système d’équations AX=B. Le système d’équations pourrait posséder une infinité de solution si :

la matrice augmentée [A|B] a une ligne de zéro
la matrice A n’a pas tous ses pivots et que la matrice augmentée échelonnée a au moins une ligne de zéro
les colonnes de la matrice A ne sont pas linéairement indépendantes et que la matrice augmentée échelonnée a au moins une ligne de zéro
les lignes de la matrice A ne sont pas linéairement indépendantes et que la matrice augmentée échelonnée au moins une ligne de zéro
si le déterminant de la matrice A est nul et que la matrice augmentée échelonnée a au moins une ligne de zéro
si la matrice A n’est pas inversible et que la matrice augmentée échelonnée a au moins une lignes de zéro
si le rang de la matrice A est plus petit que son nombre de lignes et que la matrice augmentée échelonnée a au moins une ligne de 0

Le système ne possède aucune solution

Soit un système d’équations AX=B. Le système ne possède aucune solution s’il ne possède pas de solution unique ou une infinité de solutions.

Application de la méthode de Gauss

Dans l’exemple suivant, trouvez la solution du système d’équations en vous servant des étapes de résolutions présentées ci-dessus.

Nous nous attarderons sur la résolution du système proprement dit à partir de la matrice augmentée échelonnée puisque à ce stade vous êtes supposé être confortable à échelonner les matrices.

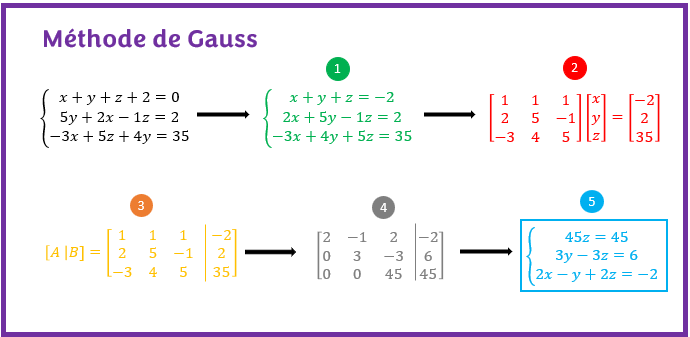
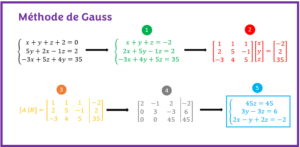
Étape 1 de la méthode de Gauss _ Ordonner les matrices

Dans cet étapes, il convient de réordonner les équations afin de faire apparaître les inconnues dans le même ordre dans toutes les équations. Ceci facilitera l’étape suivante :

Étape 1 de la méthode de Gauss _ Ordonner les équations du système

Maintenant, on observe que dans chaque équation, l’ordre des inconnues ou variables est x, y et enfin z ce qui n’était pas le cas dans le système de départ.

Étape 2 de la méthode de Gauss _ transformer le système sous la forme AX=B

Il est plus facile de transformer un système sous la forme AX=B lorsque les équations du système sont classés dans l’ordre. Les coefficients des inconnues deviennent les coefficients de la matrice A et le second membre de l’égalité devient la matrice B. En ce qui concerne la matrice X, elle est la matrice colonne des inconnues du système.

La matrice A a toujours le même nombre de lignes que le nombre d’équations du système et le même nombre de colonnes que le nombre d’inconnues du système. La matrice X est toujours la matrice colonne qui contient toutes les inconnues du système. Quant à la matrice B, elle contient toujours tout le second membre du système. Elle a donc toujours autant de lignes que le système d’équations en a.

Les détails plus approfondis de cette étape se trouvent dans l’article comment transformer un système sous la forme AX=B?

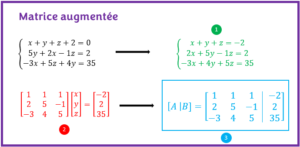
Étape 3 de la méthode de Gauss _ Écrire la matrice augmentée [A|B] du système

La matrice augmentée [A|B] d’un système consiste à fusionner la matrice A et la matrice B d’un système en une seule matrice.

Étape 3 de la méthode de Gauss _ Écrire la matrice augmentée du système

Remarquez que les matrices A et B sont les mêmes qu’a l’étape précédente. Elles ont juste été rassemblé dans une même matrice. Le trait verticale permet de séparer la matrice A et B.

Les détails plus approfondies de cette étape se trouve dans l’article de la matrice augmentée d’un système.

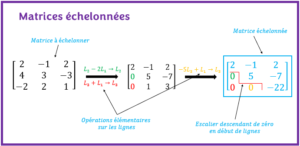
Étape 4 de la méthode de Gauss _ Écrire la matrice augmentée échelonnée en échelonnant la matrice augmentée

Dans cette étape, il faut échelonner la matrice augmentée construite à l’étape précédente en se servant uniquement des trois opérations élémentaires.

Écrire la matrice augmentée échelonnée du système

La matrice obtenue à cette étape est appelée la matrice augmentée échelonnée.

Étape 5 de la méthode de Gauss _ Résoudre le nouveau système d’équations du bas vers le haut

ici, il convient de résoudre l’équation découlant de la matrice augmentée échelonnée du système du bas vers le haut. À partir de la dernière équation, on trouve la valeur de l’inconnue z. Puis, en ce servant de la deuxième équation et connaissant la valeur de z, on peut donc déduire la valeur de la variable y. Enfin, la première équation nous permet d’obtenir x connaissant les valeurs de y et z obtenu précédemment.

Conseils et astuces

La méthode de Gauss est une technique de résolution des systèmes d’équations linéaires
La méthode de Gauss consiste résoudre le système de la matrice augmentée échelonnée du système
Un système d’équations a 3 trois types de solutions : une unique solution, une infinité de solutions et aucune solution
La matrice augmentée échelonnée d’un système d’équations n’est pas unique, car elle dépend des opérations élémentaires sur les lignes
La méthode de Gauss permet de résoudre un système d’équations par la méthode la matrice échelonnée
Le système d’équations a une unique solution si la matrice augmentée échelonnée du système a tous ses pivots : on dit que la matrice est plein rang.
Le système d’équations a une infinité de solution si la matrice augmentée échelonnée du système a une ou plusieurs lignes de zéros
Utiliser le calculateur en ligne symbolab pour vos calculs matriciels.
Si vous ne comprenez toujours pas, demandez l’assistance d’un tuteur.

FAQ

Comment faire la méthode de Gauss?

Pour résoudre un système d’équations linéaires, on peut utiliser la méthode de Gauss en respectant les cinq étapes suivantes :
– Réorganiser les équations du système pour avoir le même ordre d’apparition des variables dans chaque équations
– Transformer le système d’équations sous la forme AX=B
– Écrire la matrice augmentée [A|B] du système
– Obtenir la matrice augmentée échelonnée
– Résoudre le nouveau système d’équations du bas vers le haut Étapes de résolutions d'un système d'équations par la méthode de Gauss

Quelles sont les trois opérations autorisées dans la méthode de Gauss?

Les trois opérations autorisées dans la méthode de Gauss sont la permutation de lignes, la multiplication d’une ligne par un scalaire et l’ajout à une ligne un multiple d’une autre ligne. Opérations élémentaires sur les lignes