MATRICES ÉCHELONNÉES

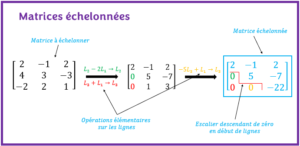
L’objectif est d’apprendre à échelonner une matrice et à reconnaître les matrices échelonnées à l’aide d’exercices résolus.

Sommaire

Rappel et mise en contexte

Une matrice est un tableau contenant un ensemble de nombres. Soit une matrice A contenant m lignes et n colonnes. On dit donc que la matrice A est de dimension m x n et on note A_mxn. En fonction du nombre de lignes et de colonnes de la matrice, on distingue deux grandes familles :

• Les matrices carrées qui ont le même nombre de lignes et de colonnes
• Les matrices rectangulaires qui ont un nombre de ligne et de colonnes différent.

Il existe bien évidement plusieurs matrices particulières. Ces matrices ont déjà été présenté dans l’article sur le langage matriciel. Les éléments d’une matrice A sont appelés coefficients et se notent a_ij où i représente le numéro de la ligne et j le numéro de la colonne du coefficient correspondant. L’élément de la première ligne et troisième colonne est donc a₁₃.

De nombreuses opérations peuvent être réaliser avec des matrices : l’addition des matrices, la soustraction des matrices, la multiplication des matrices, l’inverse d’une matrice, la transposée d’une matrice et le déterminant d’une matrice pour ne citer que ceux-là.

Aujourd’hui, nous allons découvrir la matrice échelonnée qui permettra de résoudre facilement les systèmes d’équations linéaires par la méthode de Gauss.

Forme générale des matrices échelonnées

Une matrice est dite échelonnée si le nombre de zéros précédant la première entrée non nulle de chaque ligne augmente de ligne en ligne jusqu’à n’avoir possiblement que des lignes de zéros. En d’autres termes, le nombre de zéros au début d’une ligne doit augmenter à mesure que le nombre de lignes augmente.

Pour mieux comprendre, les matrices échelonnées ont la forme générale suivantes :

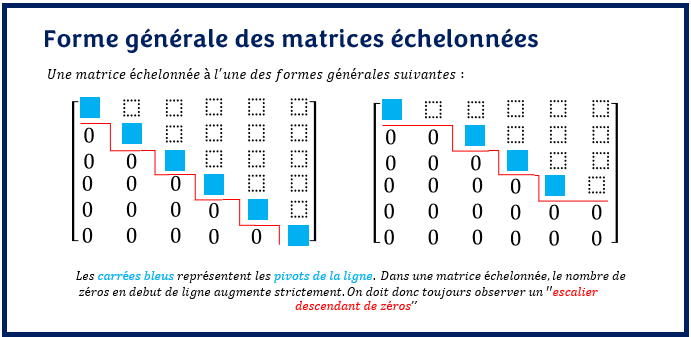
Comment reconnaitre des matrices échelonnées?

Une matrice échelonnée a la particularité d’avoir beaucoup de zéros en début de ligne. Dans toutes matrices échelonnée, le nombre de zéro en début de ligne augmente d’une ligne à l’autre. Toutes matrices qui ne respectent pas cette règle ne sont pas des matrices échelonnées.

Une matrice est appelée matrice échelonnée si le nombre de zéros précédents le premier chiffre non nul de chaque ligne augmente de ligne en ligne jusqu’à n’avoir possiblement que des lignes de zéro. Plus simplement, dans une matrice échelonnée, le nombre de zéros en début de ligne augmente de ligne en ligne sous la forme d’escalier descendant de zéros.

Dans une matrice échelonnée, le premier élément non nul d’une ligne s’appelle le pivot de la ligne. Une matrice non nulle a donc toujours au moins un pivot. Le nombre de pivot dans une matrice est toujours plus petit ou égale que le nombre de lignes et le nombre de colonnes de la matrice. Le nombre de pivot de la matrice échelonnée est le rang de la matrice. On note rang(A).

Exemples de matrices échelonnées

Voici quelques exemples de matrices échelonnées, essayer de valider par vous même!

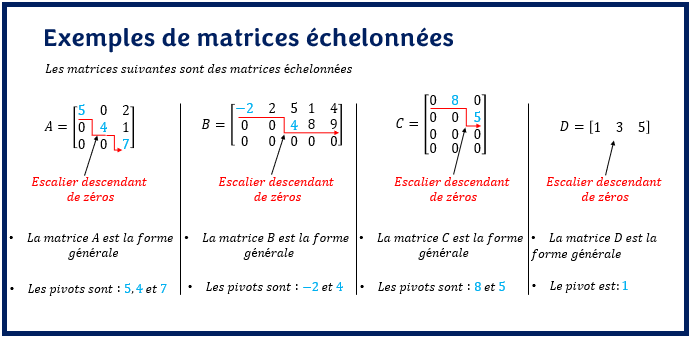
Pour la matrice A, il y’a 0 zéro au début la première ligne, 1 zéro au début de la deuxième ligne et 2 zéros au début la troisième ligne. Le nombre de zéros est bien croissant ( »escalier descendant de zéros »), donc c’est une matrice échelonnée. Ainsi, on peut donc conclure que les nombres 5, 4 et 7 sont les pivots respectifs de la première, deuxième et troisième ligne.

La matrice B est de dimension 3 x 5, elle a donc maximum trois pivots. Il n’y a pas de zéros au début de la première ligne, il y’a 2 zéros au début de la deuxième ligne et plus de 3 zéros au début de la troisième ligne ( »escalier descendant de zéros »). Les pivots de la matrice sont : -2 pour la première ligne et 4 pour la deuxième ligne. La troisième ligne n’a pas de pivot car un pivot est non nul (différent de zéro).

Quant à la matrice C, elle a 4 lignes et 3 colonnes. Il y’a donc au maximum 3 pivots. On peut donc rapidement déduire que la matrice C pourrait être échelonnée s’il a au minimum une ligne de zéro puisque la matrice a quatre lignes. On observe qu’il y’a 1 zéro au début de la première ligne, 2 zéros au début de la deuxième ligne et deux lignes de zéros ( »escalier descendant de zéros »), donc la matrice C est une matrice échelonnée. Les pivots de la matrice sont : 8 pour la première ligne et 5 pour la deuxième ligne.

La matrice F est une matrice ligne. Il y’a donc 1 pivots au maximum. La première ligne n’a pas de zéro. On a donc une matrice échelonnée. Le pivot est 1.

Exemples de matrices non échelonnées

Les matrices non échelonnées sont des matrices dont le nombre de zéros en début de lignes n’est pas strictement croissant. S’il n’y a pas de zéros en début de lignes dans aucune ligne, la matrice n’est pas échelonnée. La matrice doit être échelonnée par parler de pivots.

En d’autres termes, si dans un exercice, on vous demande de donner les pivots de la matrice, alors la première étape sera donc d’échelonner la matrice si elle ne l’ait pas déjà.

Dans les exemples suivants, les matrices ne sont pas des matrices échelonnées :

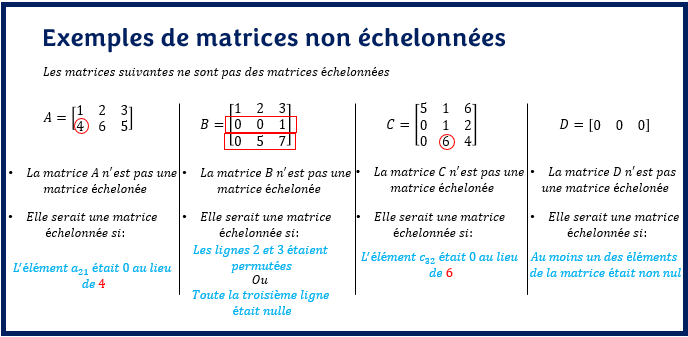
La matrice A n’est pas une matrice échelonnée car il n’ y a aucun escalier descendant de zéros. Elle serait une matrice échelonnée si l’élément a₂₁ était 0 au lieu de 4.

La matrice B est non échelonnée car il y’a plus de zéros au début de la deuxième ligne (2 zéros) par rapport à la troisième ligne (1 zéros). On n’a donc pas un escalier descendant de zéros. Elle serait une matrice échelonnée si les lignes 2 et 3 étaient permutées.

Quant à la matrice C, elle n’est pas échelonnée car il y’a le même nombre de zéros en début de la deuxième et la troisième ligne (1 zéro). La matrice C serait une matrice échelonnée si l’élément C₃₂ était 0 au lieu de 6.

En ce qui concerne la matrice D, elle n’est pas une matrice échelonnée car elle est une matrice nulle. Une matrice échelonnée doit avoir au moins un pivot or, un pivot est non nul. La matrice D serait donc une matrice échelonnée si au moins un des coefficients de la matrice est différent de zéro.

Comment échelonner une matrice?

Il est toujours possible de transformer une matrice en une matrice échelonnée en un nombre finis d’opérations. Pour transformer une matrice en une matrice échelonnée, il faut effectuer des opérations sur les lignes de la matrice.

Opérations élémentaires sur les lignes pour échelonner une matrice

Trois opérations élémentaires sont disponibles pour échelonner une matrice. Ces opérations sont :

• permuter des lignes( L_i ↔ L_j ), c’est-à-dire ( L_i → L_j ) et ( L_j → L_i ).
• multiplier une ligne par une constante k, où k ∈ ℝ et k ≠ 0
• Additionner un multiple k, où k ∈ ℝ, d’une ligne à une autre ligne ( L_i + kL_j→ L_i )

On peut également combiner ces opérations en une seule étape. Par exemple, en effectuant les opérations 2) et 3) précédentes simultanément sur les lignes L_i et L_j, nous obtenons k₁L_i + k₂L_j → L_i, où k₁ ≠ 0.

Il est interdit de permuter les colonnes ou d’effectuer des opérations entre les colonnes de la matrice.

Étapes à suivre pour échelonner une matrice

Soit une matrice A. Pour échelonner la matrice, il faut suivre les étapes suivantes :

• S’assurer que le premier élément (élément a₁₁) de la première ligne est non nul. C’est le pivot de la première ligne. S’il est nul effectué d’abord une permutation de lignes avec les lignes en dessous.
• Utiliser le pivot de la première ligne pour transformer tous les autres chiffres en dessous de lui en des zéros en utilisant la troisième opération élémentaire ( L_i + kL_j→ L_i ). L_i représente la ligne à modifier et L_j représente la ligne du pivot
• S’assurer que le deuxième élément de la deuxième ligne est non nul. C’est le pivot de la deuxième ligne. S’il est nul effectué d’abord une permutation de lignes avec les lignes en dessous.
• Utiliser le pivot de la deuxième ligne pour transformer tous les autres chiffres en dessous de lui en des zéros en utilisant la troisième opération élémentaire ( L_i + kL_j→ L_i ). L_i représente la ligne à modifier et L_j représente la ligne du pivot.
• Recommencer ces opérations avec la ligne ou les lignes suivantes.

Ces étapes peuvent être résumer en une image conceptuel :

Opérations à effectuer pour rendre un coefficient nul

Trouver l’opération à effectuer entre les lignes de la matrice ne dépends que du pivot de la ligne utilisé et du coefficient qu’on souhaite rendre nulle. Le principe est le même comme dans la méthode de résolution de système d’équation par la méthode de l’élimination (ou de réduction ou addition).

En gros, on doit multiplier la ligne du pivot par un nombre afin que le pivot devienne égale au coefficient qu’on souhaite mettre à zéro mais de signe opposés. D’où l’opération : ( L_i + kL_j→ L_i ). L_i représente la ligne à modifier et L_j représente la ligne du pivot.

On peut également multiplier la ligne du pivot par un nombre et la ligne du coefficient à mettre à zéro afin que le pivot de la ligne et le coefficient à mettre à zéro soient égaux mais de signe opposés. D’où l’opération : k₁L_i + k₂L_j → L_i, où k₁ ≠ 0, L_i représente la ligne à modifier et L_j représente la ligne du pivot.

Transformer une matrice en matrice échelonnée : Cas général

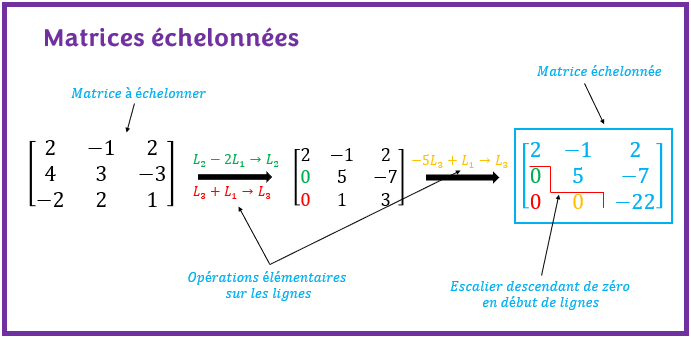
Dans l’exemple suivant, transformer la matrice sous la forme échelonnée :

Dans cet exemple, on respecte bien les étapes pour étalonner une matrice. On se sert du pivot de la ligne pour éliminer tous les coefficient en dessous de lui. Le détail de calcul de la nouvelle ligne se fait dans le brouillon. Il n’est pas nécessaire de l’inscrire dans sa copie. En réalité, c’est un calcul mental qu’on effectue chiffre après chiffre. On peut tout de même se servir d’une calculatrice pour éviter des erreurs liées au stress, à la précipitation ou autres.

Transformer une matrice en matrice échelonnée : Cas du pivot nul

Dans l’exemple suivant, transformer la matrice sous la forme échelonnée :

Dans l’exemple ci-dessus, le premier élément est nul. Il ne peut donc pas être le pivot. On effectue donc d’abord une permutation de ligne de la ligne 1 afin que le premier élément de la matrice soit non nul. Cet élément constitue donc le pivot. Noter que la permutation de ligne pourrait aussi être entre la ligne 1 et la ligne 2. La permutation entre la ligne 1 et la ligne 3 est un choix pour obtenir pivot de 1. À partir de cela, il est facile de trouver les autres opérations tout en évitant les fractions.

Transformer une matrice en matrice échelonnée : Cas d’une ligne de zéro

Dans l’exemple suivant, transformer la matrice sous la forme échelonnée :

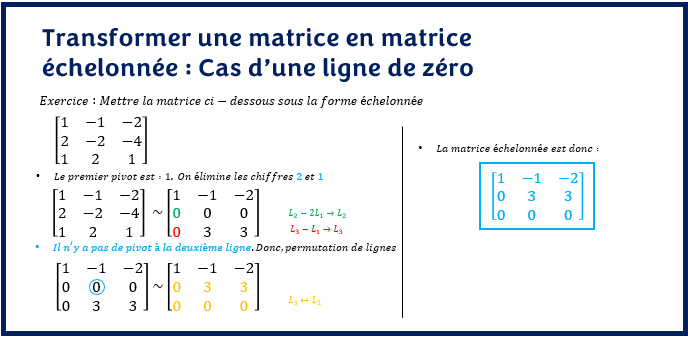
Dans l’exemple ci-dessus, après les deux premières éliminations, on constate qu’il n’a pas de pivot à la position de la deuxième ligne et deuxième colonne. On effectue donc une permutation de lignes pour que le pivot de la deuxième ligne soit non nul. La troisième ligne est une ligne de zéro, donc la matrice est directement sous la forme échelonnée.

Conseils et astuces

• Dans une matrice échelonnée, le nombre de zéros en début de ligne est strictement croissant à mesure que les lignes augmentent
• Un pivot est le premier élément non nul sur une ligne dans la matrice échelonnée
• Toute matrice est transformable en matrice échelonnée en un nombre fini d’opérations
• Il est interdit d’effectuer des opérations élémentaires entre les colonnes d’une matrice
• Une matrice nulle n’est pas une matrice échelonnée
• La matrice échelonnée s’utilise pour faciliter la résolution des systèmes d’équations linéaires
• Le rang de la matrice échelonnée est égal au nombre de pivots de la matrice échelonnée.
• Utiliser Symbolab pour effectuer vos calculs matriciels
• Demander l’assistance d’un tuteur au besoin

FAQ sur les matrices échelonnées

Sujets similaires

• 
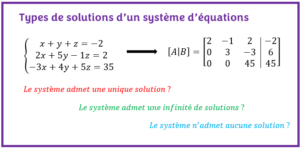
  COMMENT SAVOIR SI UN SYSTÈME ADMET UNE SOLUTION
  Découvrez les trois types de solutions d’un système. Apprenez comment savoir si un système admet des solutions avec des exercices résolus.
• 
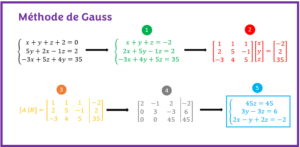
  MÉTHODE DE GAUSS
  L’objectif est d’apprendre à résoudre un système d’équations linéaires par la méthode de Gauss à partir d’exercices résolus.
• 
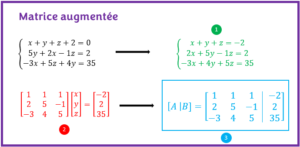
  MATRICE AUGMENTÉE
  L’objectif est d’apprendre à écrire la matrice augmentée d’un système d’équations et de l’échelonner à l’aide d’exercices résolus.
• 
  MATRICES ÉCHELONNÉES
  L’objectif est d’apprendre à échelonner une matrice et à reconnaître les matrices échelonnées à l’aide d’exercices résolus.
• 
  FORME AX=B : TRANSFORMER UN SYSTÈME D’ÉQUATIONS LINÉAIRES
  L’objectif est d’apprendre comment transformer un système d’équations linéaires sous la forme AX=B avec des exercices résolus.
• 
  MÉTHODE PAR ÉLIMINATION
  L’objectif est d’apprendre à résoudre un système d’équations linéaires par la méthode d’élimination avec des exercices résolus.
• 
  MÉTHODE DE SUBSTITUTION
  L’objectif est d’apprendre à résoudre un système d’équations linéaires par la méthode de substitution avec des exercices résolus.
• 
  MÉTHODE DE COMPARAISON
  L’objectif est d’apprendre à résoudre un système d’équations linéaires par la méthode de comparaison avec des exercices résolus.