Périmètre d’un losange

L’objectif est d’apprendre à calculer le périmètre d’un losange et de connaitre ses propriétés avec des exemples résolus.

Sommaire

Rappel et mise en contexte

Un quadrilatère est une figure géométrique a quatre côtés et qui possèdent une grande diagonale et un petite diagonale. De plus, si l’on additionne tous les angles intérieur du quadrilatère, on obtient la valeur de 360 degrés. Il existe 6 autres types de quadrilatères : losange, rectangle, carré, trapèze et parallélogramme.

Le losange est défini comme un type de quadrilatère, ainsi qu’un type spécial de parallélogramme. Tous les côtés opposés d’un losange sont parallèles et tous les angles opposés sont égaux. De plus, les quatre côtés d’un losange ont la même longueur. Toutes les diagonales d’un losange se coupent en deux et forment un angle droit.

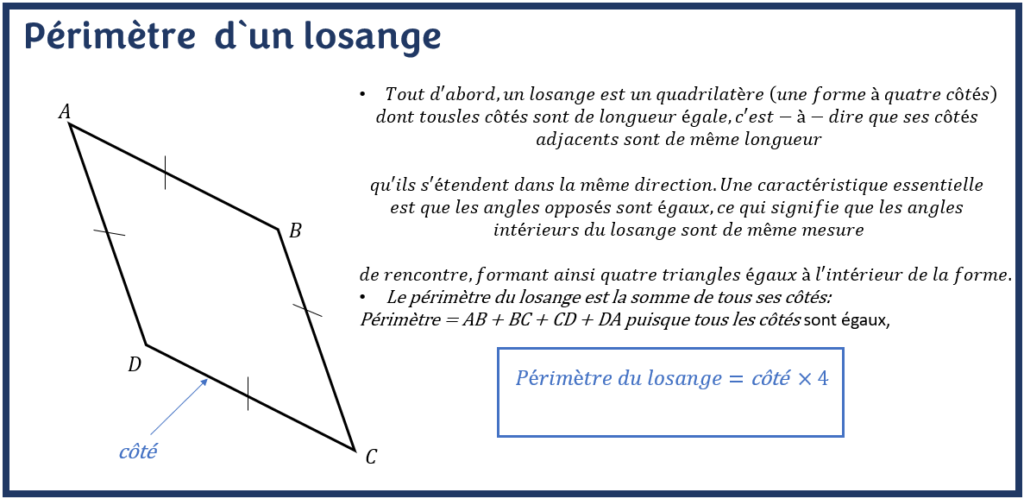
La région couverte par un losange dans un plan bidimensionnel est connue sous le nom d’aire d’un losange. La longueur totale des limites d’une forme en losange est son périmètre. En termes plus simples, la somme des quatre côtés d’un losange est appelée son périmètre.

Périmètre d’un losange

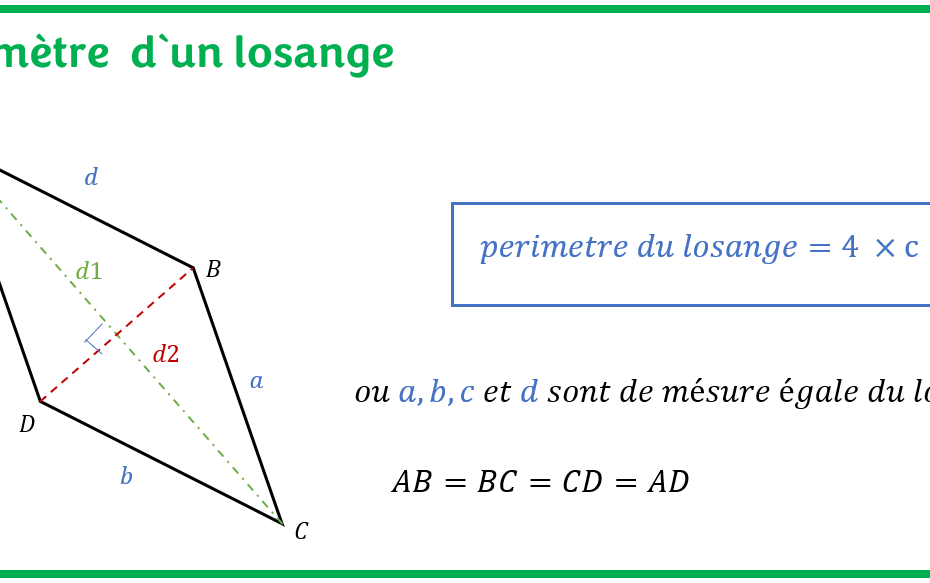
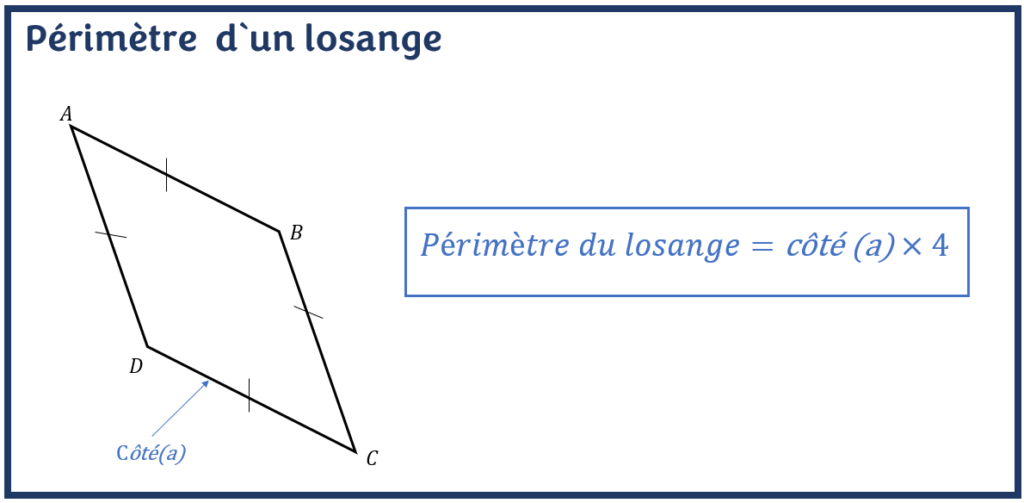
La longueur totale des limites d’une forme en losange est son périmètre. En termes plus simples, la somme des quatre côtés d’un losange est appelée son périmètre. Voici la formule pour trouver le périmètre :

Le périmètre d’un Losange = P = 4a unités

Dans cette formule, « a » est le côté.

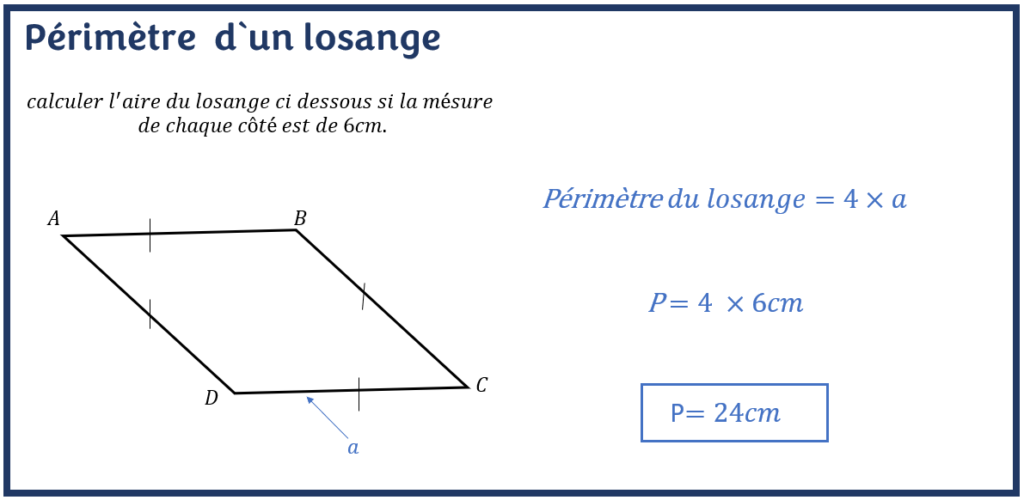
Exemple de calcul du périmètre d`un losange

calculer l′ aire du losange ci dessous si la mesure de chaque côté est de 6cm.

Exemple de calcul du périmètre d`un losange lorsqu´on connais les mesures des diagonales

Un losange est un parallélogramme dont tous les côtés sont égaux. Un carré est un losange dont tous les angles et tous les côtés sont égaux. Les carrés et les losanges ont des bissectrices diagonales perpendiculaires qui divisent chaque diagonale en 2 morceaux égaux, et divisent également le quadrilatère en 4 triangles rectangles égaux.

nous savons que le théorème de Pythagore fonctionnerait très bien dans cette situation, en utilisant la moitié de chaque diagonale comme deux branches du triangle rectangle AoB.

(3,5cm)²+(2,5cm)²=h² où h est l’hypoténuse.

h=4,3cm

Puisque l’hypoténuse de chaque triangle est un côté du losange, nous avons trouvé ce dont nous avons besoin pour trouver le périmètre.

P=4,3 ×4

P=17,20cm

Conseils et astuces relative au périmètre d`un losange

• Tous les côtés d’un losange seront toujours égaux.
• Tous les côtés opposés d’un losange sont parallèles entre eux.
• Tous les angles opposés d’un losange seront égaux.
• Toutes les diagonales d’un losange se couperont toujours à angle droit.
• Toutes les diagonales coupent les angles en deux.
• Après avoir additionné deux angles adjacents, vous obtiendrez une somme de 180 degrés.
• Dans un losange, deux diagonales peuvent former quatre triangles rectangles.
• Lorsque vous joignez le milieu des côtés d’un losange, vous pouvez former un rectangle.
• Si vous joignez les milieux à partir de la moitié de la diagonale, vous pouvez former un autre Losange !
• Vous ne pouvez former aucune sorte de cercle circonscrit autour d’un losange.
• Vous ne pouvez former aucun cercle d’inscription à l’intérieur d’un losange.
• Lorsque vous joignez les milieux des quatre côtés d’un losange, vous formerez un rectangle. Cependant, la largeur et la longueur de ce rectangle seront la moitié de la diagonale. Finalement, l’aire de ce rectangle sera la moitié de l’aire du losange.
• Consulter la vidéo sur le périmètre d’un losange au besoin.

FAQ

Sujets similaires

• 
  Périmètre d’un losange
  L’objectif est d’apprendre à calculer le périmètre d’un losange et de connaitre ses propriétés avec des exemples résolus.
• 
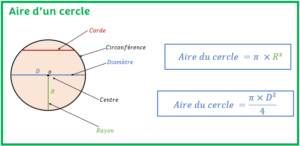
  Aire d’un cercle
  L’objectif est d’apprendre comment calculer l’aire d’un cercle et de connaitre ses propriétés avec des exemples résolus.
• 
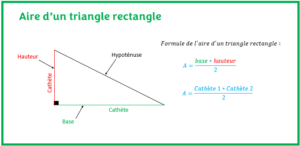
  Aire d’un triangle rectangle
  L’objectif est d’apprendre comment calculer l’aire d’un triangle rectangle de plusieurs façons différentes avec des exercices résolus.
• 
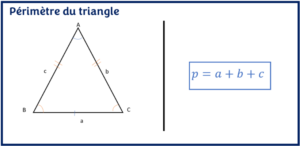
  Périmètre du triangle
  L’objectif est d’apprendre à calculer le périmètre du triangle et de connaître ses propriétés à partir d’exercices résolus.