SYSTÈME D’ÉQUATIONS LINÉAIRES

L’objectif est d’apprendre à reconnaître et déterminer l’ensemble de solution d’un système d’équations linéaires avec des exemples résolus.

Sommaire

Rappel et mise en contexte

Une équation linéaire est une équation où toutes les variables sont de degré 1. Les équations linéaires se présentent sous la forme a₁x₁ + a₂x₂ + a₃x₃ + …+ a_nx_n = b. où les x₁, x₂,…,x_n sont les variables et les a₁,a₂,…,a_n sont les coefficients constants respectifs et b est aussi constant.

Une équation linéaire est aussi une équation qui ne possède pas des termes non linéaires. Ces termes non linéaires peuvent donc être :

• des fonctions polynomiales de degré n supérieur à 1(n positif)( xⁿ)
• des fonctions trigonométriques(cos x, sin x, tan x, sec x, cotan x, cosec x),
• des racines n-ièmes(n√x),
• des produits de variables (xy, xz,yz,xyz, etc),
• des variables avec des exposants négatifs (n positifs)(x^-n, 1/xⁿ),
• des fonctions exponentielles(e^x,e^xy, etc)
• des fonctions logarithmiques(ln x, log x, log xy, etc.).

Voici quelques exemples d’équations linéaires et non linéaire.

Consulter le cours sur les équations linéaires pour en savoir plus.

Un système d’équations linéaires sont un regroupement de plusieurs d’équations linéaires. Dans cet article, nous allons surtout présenter la définition d’un système d’équations linéaires et son ensemble de solution.

Définition d’un système d’équations linéaires

Supposons qu’une équation linéaire a n variables et que l’on dispose de m équations linéaires, alors on peut former un système d’équations linéaires de m équations linéaires à n inconnues.

Les coefficients d’une équations linéaires sont des chiffres et donc des constantes.

Exemples d’un système d’équations linéaires

Voici quelques exemples de systèmes d’équations linéaires. Pour chacun d’eux, identifiez les nombres d’équations et le nombre de variables.

Dans le premier exemple, la première équation semble ne pas avoir de coefficients et pourtant il y’en a. Si aucun coefficient n’est écrit alors, il vaut 1.

Dans le deuxième cas, la première équation n’a pas la variable z donc son coefficient associé est 0 car 0*z = 0. La dernière équation n’a pas la variable x donc son coefficient associé est 0 car 0*x = 0. Ce système d’équations linéaires a tout de même 3 variables au moins l’une de ses équations contient les variables x, y ou z.

Le troisième exemple a deux équations et les coefficients de la première équation sont : 1 , -1 et -1 car les coefficients n’ont pas été mentionnés (1*x = x , -1*y = -y, ou -1*z = -z).

Solution d’un système d’équations linéaires

Une solution d’une équation linéaire est une série de nombre qui permet d’obtenir une égalité vraie entre les deux membres de l’équation.

Similairement, une solution d’un système d’équations linéaires est une série de nombre (n-uplet)qui permet d’obtenir une égalité vraie entre les deux membres de chacune des équations du système d’équations simultanément.

La solution d’un système d’équations linéaires est noté par un n-uplet ordonné : (s₁, s₂, s₃, … , s_n) .

Comment montrer qu’un couple est solution d’un système?

Un couple est solution d’un système s’il y a une égalité vraie entre les deux membres de toutes les équations du système d’équations linéaires en le remplaçant dans le système. Regardons ensemble l’exemple suivant :

Ensemble de solution d’un système d’équations linéaires

L’ensemble de solution d’une équation linéaire est l’ensemble de toutes les solutions possibles de l’équation linéaire.

Similairement, l’ensemble de solution d’un système d’équations linéaires est l’ensemble de toutes les solutions du système d’équations. Pour trouver l’ensemble de solution d’un système d’équations, il faut le résoudre.

Nous allons voir dans un autre cours comment résoudre un système d’équations linéaires. Il existe plusieurs méthodes de résolution d’un système d’équations: méthode de Gauss, méthode de Gauss-Jordan, méthode utilisant l’inverse d’une matrice et la méthode de Cramer. Toutes ces techniques seront abordées dans d’autres articles.

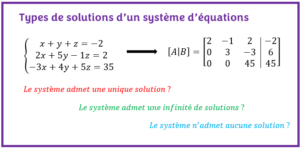
Types de solution d’un système d’équations linéaires

Un système d’équations linéaire ne possède pas toujours une solution. En effet, lorsqu’on résous un système d’équation, l’on peut obtenir 3 types de solutions possibles :

• Une solution unique : la solution du système admet une seule réponse
• Une infinité de solutions : le système d’équations admet plus d’une solution
• Aucune solution : il n’est pas possible de trouver un couple de nombre qui satisfait simultanément à toutes les équations du système d’équations linéaires.

Un système d’équations linéaires est compatible lorsqu’il a au moins une solution. On parle aussi de système d’équation cohérent ou de système d’équation non contradictoire.

Un système d’équations linéaires est incompatible lorsqu’il n’a aucune solution. On parle aussi de système d’équation incohérent ou de système d’équation contradictoire.

Nous y reviendrons plus spécifiquement lorsque nous verrons les techniques de résolutions des systèmes d’équations.

Systèmes d’équations linéaires équivalents

Deux systèmes d’équations linéaires à n variables sont des systèmes équivalents si les deux systèmes ont le même ensemble solution.

En d’autres termes, deux systèmes d’équations sont équivalents si l’on est capable de transformer l’un des systèmes d’équations pour obtenir l’autre système d’équation à partir d’opérations élémentaires.

Ces opérations élémentaires sont :

• Permuter des équations (E_i ↔ E_j), c’est-à-dire (E_i → E_j )et (E_j → E_i)
• Multiplier les deux membres d’équation par une constante k, où k∈ IR et k≠0 (kE_i → E_i)
• Additionner, membre à membre, à une équation une autre équation dont les deux membres ont été multipliés par k, où k∈ IR (E_i + kE_j→E_i)

Conseils et astuces concernant un système d’équations linéaires

• Un système d’équations est un ensemble de plusieurs équations à résoudre simultanément.
• Une équation linéaire est est une équation qui ne contient pas des termes non linéaires.
• Une solution d’un système d’équations est un couple qui rends vrai toutes les égalités de chaque équation du système simultanément.
• L’ensemble de solutions d’un système d’équations est l’ensemble de toutes les solutions possibles. On l’obtient en résolvant le système d’équations.
• Trois types de solutions sont possibles lorsqu’on résout un système d’équations : unique solution, infinité de solutions et aucune solution.
• Des systèmes d’équations sont équivalents si par des opérations élémentaires, on obtient le même système d’équation. Simplement, si deux systèmes d’équations linéaires ont le même ensemble de solution, alors ils sont équivalents.
• Un système d’équation qui admet une solution ou une infinité de solution est dit compatible ou cohérent ou non contradictoire.
• Un système d’équation qui n’a aucune solution est dit incompatible ou incohérent ou contradictoire.
• Il existe des méthodes pour résoudre un système d’équations : la méthode de comparaison, la méthode de substitution, la méthode d’élimination, la méthode de Gauss, la méthode de Gauss-Jordan, la méthode de la matrice inverse.
• Utilisez le logiciel symbolab pour vos calcul au besoin et demander l’assistance d’un tuteur au besoin.

Sujets similaires

• 
  COMMENT SAVOIR SI UN SYSTÈME ADMET UNE SOLUTION
  Découvrez les trois types de solutions d’un système. Apprenez comment savoir si un système admet des solutions avec des exercices résolus.
• 
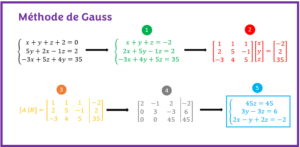
  MÉTHODE DE GAUSS
  L’objectif est d’apprendre à résoudre un système d’équations linéaires par la méthode de Gauss à partir d’exercices résolus.
• 
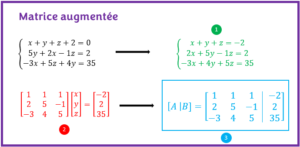
  MATRICE AUGMENTÉE
  L’objectif est d’apprendre à écrire la matrice augmentée d’un système d’équations et de l’échelonner à l’aide d’exercices résolus.
• 
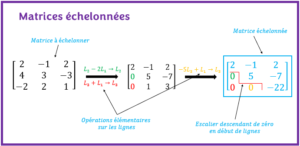
  MATRICES ÉCHELONNÉES
  L’objectif est d’apprendre à échelonner une matrice et à reconnaître les matrices échelonnées à l’aide d’exercices résolus.
• 
  FORME AX=B : TRANSFORMER UN SYSTÈME D’ÉQUATIONS LINÉAIRES
  L’objectif est d’apprendre comment transformer un système d’équations linéaires sous la forme AX=B avec des exercices résolus.
• 
  MÉTHODE PAR ÉLIMINATION
  L’objectif est d’apprendre à résoudre un système d’équations linéaires par la méthode d’élimination avec des exercices résolus.
• 
  MÉTHODE DE SUBSTITUTION
  L’objectif est d’apprendre à résoudre un système d’équations linéaires par la méthode de substitution avec des exercices résolus.
• 
  MÉTHODE DE COMPARAISON
  L’objectif est d’apprendre à résoudre un système d’équations linéaires par la méthode de comparaison avec des exercices résolus.