MÉTHODE DE COMPARAISON

L’objectif est d’apprendre à résoudre un système d’équations linéaires par la méthode de comparaison avec des exercices résolus.

Sommaire

Rappel et mise en contexte

Un système d’équations linéaires est un ensemble de plusieurs équations linéaires. La solution d’un système d’équations linéaires est un couple de nombres qui satisfait simultanément toutes les équations linéaires du système d’équations linéaires.

Il existe plusieurs méthodes pour résoudre un système d’équations linéaires. Nous avons les méthodes élémentaires que nous avons déjà rencontrées au secondaire à savoir : la méthode de comparaison, la méthode de substitution et la méthode d’élimination. Il existe aussi des méthodes plus approfondies qui correspondent au niveau cégep à savoir : la méthode de Gauss, la méthode de Gauss-Jordan, la méthode d’inversion de matrices carrées. Bien sûr, il existe encore des méthodes plus avancées qui correspondent au niveau universitaire.

Dans cet article, on s’intéressera uniquement à la méthode de comparaison pour la résolution du système d’équations linéaires.

Principe de la méthode de comparaison

Résoudre un système d’équations linéaires revient à trouver son ensemble de solution. À cet égard, utilisez la méthode de comparaison.

C’est une technique très simple utilisée lorsqu’on a un système de deux équations à résoudre. Cette méthode consiste à isoler la même variable de deux équations et de les égaliser.

Étapes de résolution par la méthode de comparaison

Les étapes suivantes décrivent comment trouver l’ensemble de solution d’un système d’équations linéaires en utilisant la méthode de comparaison:

• Isoler une même variable de votre choix dans la première équation
• Isoler la même variable choisie dans la deuxième équation
• Égaliser les deux expressions obtenues aux deux premières étapes correspondant à la variable isolée
• Résoudre l’équation obtenue à l’étape 3 en isolant la variable restante
• Calculer la valeur de la variable isolée(étape 1 ou 2) dans la première étape en se servant du résultat de l’étape 4.
• Écrire l’ensemble de solution du système d’équations linéaires

Résolution d’un système d’équations linéaires par la méthode de comparaison

Appliquons les étapes précédentes de résolution dans l’exemple ci-dessous:

Au regard des étapes précédentes, on voit que la variable que l’on a choisi d’isoler à l’étape 1 est x. Puis, en suivant le reste des étapes, on trouve d’abord la valeur de y et ensuite la valeur de x. Il est important de préciser que le résultat n’aurait pas été différent si à la première étape l’on avait choisi d’isoler y. Dans ce cas, en suivant le reste des étapes, on trouverait d’abord la valeur de x et ensuite la valeur de y. Faites l’exercice!

Vérification de la solution d’un système d’équations linéaires

Lorsque l’on résout un système d’équations linéaires, l’on peut toujours vérifier si l’ensemble de solutions obtenu est correct. Pour cela, il suffit de remplacer les valeurs des variables x et y obtenues dans chacune des équations constituant le système d’équations.

Si au moins une des équations du système ne fait pas de sens (équation fausse ou absurde), alors l’ensemble de solutions obtenues est faux (une erreur s’est glissée dans les calculs). SI toutes les équations du système d’équations sont vraies (équations logiques), alors l’ensemble de solutions obtenues correspond bien à l’ensemble de solutions du système.

Un système d’équations linéaires qui admet au moins une solution est dit compatible (cohérent ou non contradictoire).

Un système d’équations linéaires qui n’a aucune solution est dit incompatible (incohérent ou contradictoire).

Conseils et astuces concernant la méthode de comparaison

• Un système d’équations linéaires est un ensemble d’équations linéaires
• Résoudre un système d’équations linéaires revient à trouver son ensemble de solution
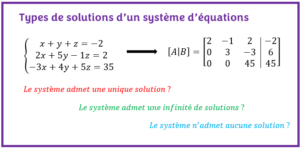
• Trois types de solutions peuvent être obtenues lorsqu’on résous un système d’équations
• La méthode de comparaison permet de résoudre un système d’équations linéaires
• Les méthodes élémentaires de résolution de systèmes d’équations linéaires sont : la méthode de comparaison, la méthode de substitution et la méthode d’élimination
• Il est important de faire une vérification après la résolution d’une équation linéaire
• Un système d’équations linéaires est compatible lorsqu’il a au moins une solution
• Un système d’équations linéaires est incompatible lorsqu’il n’a aucune solution
• Demander l’assistance d’un tuteur au besoin.
• Prochain article : Résolution d’un système d’équations linéaires : Méthode de substitution

FAQ concernant la méthode de comparaison

Sujets similaires

• 
  COMMENT SAVOIR SI UN SYSTÈME ADMET UNE SOLUTION
  Découvrez les trois types de solutions d’un système. Apprenez comment savoir si un système admet des solutions avec des exercices résolus.
• 
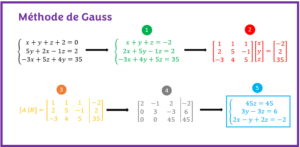
  MÉTHODE DE GAUSS
  L’objectif est d’apprendre à résoudre un système d’équations linéaires par la méthode de Gauss à partir d’exercices résolus.
• 
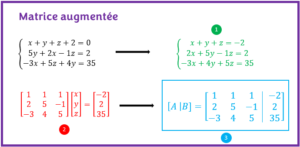
  MATRICE AUGMENTÉE
  L’objectif est d’apprendre à écrire la matrice augmentée d’un système d’équations et de l’échelonner à l’aide d’exercices résolus.
• 
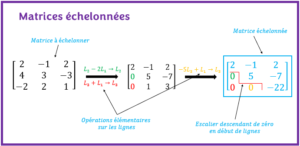
  MATRICES ÉCHELONNÉES
  L’objectif est d’apprendre à échelonner une matrice et à reconnaître les matrices échelonnées à l’aide d’exercices résolus.
• 
  FORME AX=B : TRANSFORMER UN SYSTÈME D’ÉQUATIONS LINÉAIRES
  L’objectif est d’apprendre comment transformer un système d’équations linéaires sous la forme AX=B avec des exercices résolus.
• 
  MÉTHODE PAR ÉLIMINATION
  L’objectif est d’apprendre à résoudre un système d’équations linéaires par la méthode d’élimination avec des exercices résolus.
• 
  MÉTHODE DE SUBSTITUTION
  L’objectif est d’apprendre à résoudre un système d’équations linéaires par la méthode de substitution avec des exercices résolus.
• 
  MÉTHODE DE COMPARAISON
  L’objectif est d’apprendre à résoudre un système d’équations linéaires par la méthode de comparaison avec des exercices résolus.