L’objectif est d’apprendre à résoudre un système d’équations linéaires par la méthode par élimination avec des exercices résolus.
Sommaire
Rappel et mise en contexte
Jusqu’ici dans les précédents articles, nous avons présenté déjà deux méthodes élémentaires pour résoudre un système d’équations linéaires. Il s’agit de la méthode de comparaison et la méthode de substitution. Dans cet article, on s’intéressera à la dernière méthode de base à savoir la méthode d’élimination.
Nous avons vu que chaque méthode à sa particularité et ses étapes à suivre. En fonction de l’exercice, il est souvent plus facile d’utiliser une méthode par rapport aux autres. La méthode de substitution étant la plus robuste peu importe le système d’équations.
Dans les articles suivants, nous verrons d’autres techniques de résolution des systèmes d’équations linéaires plus avancées : la méthode de Gauss, la méthode de Gauss-Jordan et la méthode de la matrice inverse.
Principe de la méthode par élimination
La méthode d’élimination comme son nom l’indique consiste à éliminer des variables pour n’en garder qu’une seule. De cette façon, on obtient une simple équation linéaire facile à résoudre. Cette méthode est encore appelée méthode d’addition ou méthode de réduction. Vous allez comprendre pourquoi.
Comme toutes les autres méthodes de résolution de système, la méthode d’élimination a des étapes qu’il faut respecter.
Étapes de résolution d’un système d’équations linéaires par la méthode par élimination
La méthode d’élimination se distingue des autres méthodes par les étapes suivantes :
- Choisir la variable à éliminer en premier
- Multiplier chaque équation par un chiffre afin que la variable à éliminer ait des coefficients opposés
- Additionner membre à membre les équations pour éliminer la variable choisie à l’étape 1
- Résoudre l’équation obtenue à l’étape 3
- Substituer la valeur obtenue à l’étape 4 dans l’une des équations du système et trouver la valeur des autres variables.
- Écrire l’ensemble de solutions du système d’équations linéaires
Résolution d’un système d’équations linéaires par la méthode par élimination
Appliquons les étapes précédentes de résolution dans l’exemple ci-dessous:
Dans l’exemple précèdent, on a fait le choix d’éliminer la variable x en premier pour trouver la variable y. Cela reviendrait au même si l’on avait d’abord éliminer la variable y en premier pour trouver la valeur de la variable x. Évidemment, la solution finale ne change pas peu importe la méthode utilisée.
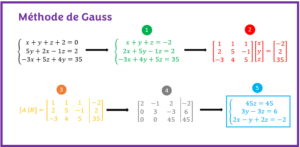
Pour les systèmes d’équation à 3 inconnues ou plus, les étapes de résolutions sont similaires:
- Choisir la variable à éliminer en premier
- Éliminer la variable choisie pour obtenir un nouveau système à deux variables : Ceci passe nécessaire nécessairement par la multiplication de chaque équation par un coefficient approprié. Utiliser la même équation dans les deux opérations. Par exemple, si on note par Ei l’équation i, alors les opérations suivantes peuvent être effectué( E2-5E1 et E3-3E1 ). E1 est appelé la ligne pivot. Nous le comprendrons mieux par la suite avec la méthode de Gauss.
- Continuer le reste des étapes pour un système d’équations à deux inconnues
Vérification de la solution d’un système d’équations linéaires
Il est toujours conseillé de valider la solution d’un système d’équation une fois résolus. Cela permet de déceler les erreurs de calcul qu’on aurait pu faire pendant la résolution.
La vérification consiste à remplacer les valeurs de chaque variable obtenues dans le système d’équation initiale. Si toutes les équations sont cohérentes, alors la solution obtenue est bonne. Si au moins une des équations donne un résultat absurde ou incohérent, alors la solution du système est fausse. Une erreur s’est glissé pendant la résolution. Vérifier vos calculs et vos démarches.
Dans notre exemple, on voit bien que toutes les équations du système donnent des résultats cohérents. Donc, l’ensemble de solutions du système est correct.
Conseils et astuces concernant la méthode par élimination
- Un ensemble de deux équations ou plus est appelée système d’équations
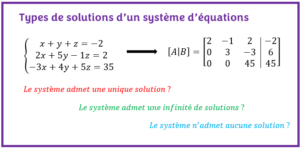
- Un système d’équations a trois types de solutions : solution unique, infinité de solutions et aucune solution
- La méthode d’élimination permet de résoudre un système d’équations linéaires
- Les méthodes élémentaires de résolution de systèmes d’équations linéaires sont : la méthode de comparaison, la méthode de substitution et la méthode d’élimination
- Il est important de faire une vérification après la résolution d’une équation linéaire
- Un système d’équations linéaires est compatible lorsqu’il a au moins une solution
- Un système d’équations linéaires est incompatible lorsqu’il n’a aucune solution
- Demander l’assistance d’un tuteur au besoin.
- Utiliser Symbolab pour vos calculs matriciels
- Prochain article : Résolution d’un système d’équations linéaires : Méthode de Gauss
FAQ concernant la méthode par élimination
La méthode d’élimination consiste à faire en sorte que les coefficients d’une des variables, dans deux équations, soient des nombres opposés : cela peut être obtenu en multipliant chaque membre d’une équation par un nombre approprié et chaque membre de l’autre équation par un autre nombre approprié.
La méthode d’élimination est encore appelée méthode d’addition ou méthode de réduction. En effet, en additionnant les deux équations, on vise éliminer une des variables pour réduire le nombre de variables de l’équation.
Sujets similaires
- COMMENT SAVOIR SI UN SYSTÈME ADMET UNE SOLUTION
Découvrez les trois types de solutions d’un système. Apprenez comment savoir si un système admet des solutions avec des exercices résolus. - MÉTHODE DE GAUSS
L’objectif est d’apprendre à résoudre un système d’équations linéaires par la méthode de Gauss à partir d’exercices résolus. - MATRICE AUGMENTÉE
L’objectif est d’apprendre à écrire la matrice augmentée d’un système d’équations et de l’échelonner à l’aide d’exercices résolus. - MATRICES ÉCHELONNÉES
L’objectif est d’apprendre à échelonner une matrice et à reconnaître les matrices échelonnées à l’aide d’exercices résolus. - FORME AX=B : TRANSFORMER UN SYSTÈME D’ÉQUATIONS LINÉAIRES
L’objectif est d’apprendre comment transformer un système d’équations linéaires sous la forme AX=B avec des exercices résolus. - MÉTHODE PAR ÉLIMINATION
L’objectif est d’apprendre à résoudre un système d’équations linéaires par la méthode d’élimination avec des exercices résolus. - MÉTHODE DE SUBSTITUTION
L’objectif est d’apprendre à résoudre un système d’équations linéaires par la méthode de substitution avec des exercices résolus. - MÉTHODE DE COMPARAISON
L’objectif est d’apprendre à résoudre un système d’équations linéaires par la méthode de comparaison avec des exercices résolus.