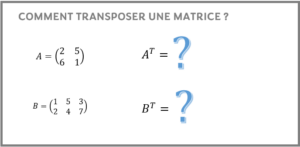
L’objectif est d’apprendre à faire la transposée d’une matrice et découvrir les propriétés relatives à la transposition de matrice avec des exercices résolus.
Sommaire
La transposée est l’une des opérations sur les matrices que nous pouvons effectuer. De même que l’addition des matrices, la soustraction de matrice ou la multiplication de matrice, la transposée d’une matrice est très utile pour diverses situations en algèbre linéaire. La transposée d’une matrice est une opération simple de permutation des lignes et des colonnes de la matrice. Elle a de nombreuses propriétés que nous allons présenter ici.
Transposée d’une matrice
La transposée d’une matrice est une matrice notée : AT. C’est l’une des opérations les plus simples sur les matrices.
Transposée d’une matrice carrée
La transposée d’une matrice carrée est une matrice carrée de même dimension. La transposition d’une matrice consiste à transformer chaque ligne de la matrice en colonne ou encore à transformer toutes les colonnes de la matrice en ligne.
Regardons ensemble l’exemple suivant :
Exemple 1:
Considérons l’exemple suivant :
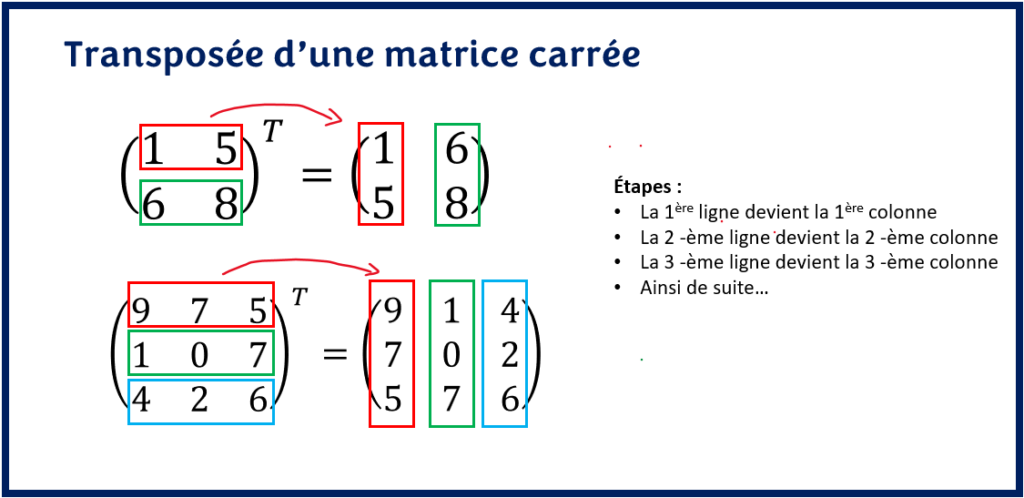
La transposée d’une matrice est sans aucun doute l’une des opérations sur les matrices la plus simple. Il suffit de prendre chaque ligne de la matrice et de l’écrire sur la colonne en respectant l’ordre apparition. Ainsi, la première ligne devient la première colonne, la deuxième ligne devient la deuxième colonne, la troisième ligne devient la troisième colonne, ainsi de suite.
Remarquez que les chiffres sur la diagonale principale de la matrice n’ont pas changé. Dans le premier cas par exemple, les éléments sur la diagonale sont : { 1 , 8} et dans le deuxième cas, les éléments sur la diagonale sont: {9, 0, 6}. Ceci est normal puisque les éléments sur la diagonale sont les coefficients aij avec le même numéro de ligne et de colonne.
Pour tout autre élément non situé sur la diagonale, la transposée de la matrice permet de permuter les positions des lignes et des colonnes. Par exemple dans le premier cas, le chiffre 5 est le coefficient a12 de la matrice. Il se trouve donc à l’intersection de la première ligne et deuxième colonne. Si on transpose donc la matrice, il deviendra le coefficient a21 c’est-à-dire le coefficient situé à l’intersection de la deuxième ligne et la première colonne. C’est justement ce qu’on observe.
Des étapes plus détaillées se trouvent dans l’article : Comment transposer une matrice?
Transposée d’une matrice rectangulaire
La transposée d’une matrice rectangulaire est une matrice rectangulaire de dimension différente. La transposition de matrice rectangulaire suit le même principe que la transposition de matrice carrée. De ce fait, on transforme toujours successivement chaque ligne de la matrice en colonne tout en respectant l’ordre d’apparition.
Exemple 2
Considérons l’exemple suivant:
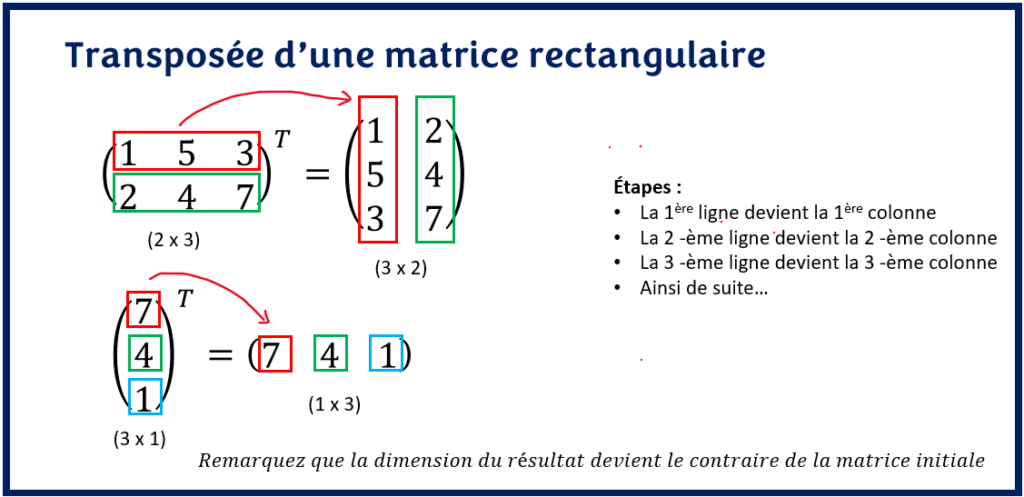
La transposée d’une matrice rectangulaire de dimension (n x m) est une matrice rectangulaire de dimension (m x n). Par exemple dans le premier cas, la dimension de la matrice initiale est (2 x 3). Après transposition de la matrice, la dimension du résultat est (3 x 2).
Une fois de plus, on transforme les lignes de la matrice en colonne. Puisque dans ce cas, le nombre de lignes est différent du nombre de colonnes, on obtient donc une matrice de dimension différente de la matrice initiale.
Des étapes plus détaillées se trouvent dans l’article : Comment transposer une matrice?
Propriétés de la transposée d’une matrice
La transposition de matrice obéit à plusieurs propriétés parmi lesquelles :
Propriété 1: (AT)T= A
Transposer deux fois une matrice permet de revenir à la matrice elle-même.
Exemple 3
Considérons l’exemple suivant:

On remarque que la double transposition permet de revenir à la matrice initiale. C’est pourquoi, cette propriété est très utile lorsqu’il s’agit de simplifier des équations qui contiennent des transpositions de matrice.
Propriété 2: (αA)T=α.AT
La transposée de la multiplication d’une matrice par un scalaire est le produit du scalaire par la matrice transposée.
Exemple 4
Considérons l’exemple suivant:

On voit qu’il est tout à fait possible de faire le produit d’une matrice par un scalaire avant de la transposer. On obtient le même résultat si l’on transpose premièrement la matrice avant de la multiplier par le scalaire. Cette propriété est très utile dans les exercices de démonstrations.
Propriété 3: (A+B)T=AT+BT
La transposée de la somme de deux matrices ou encore la transposition d’une somme de plusieurs matrices est la somme de la transposée de chacune des matrices.
Exemple 5
Considérons l’exemple suivant:

Propriété très utile pour simplifier des opérations matricielles, elle permet de se défaire des parenthèses. On voit bien que si on additionne deux matrices et ensuite on transpose le résultat, on obtient le même résultat en additionnant la transposée de chacune de ces matrices. Cette propriété est aussi valable pour la transposition de la soustraction de matrice.
Vous pouvez trouver comment additionner deux matrices dans la série de cours sur l’algèbre linéaire.
Propriété 4: (AB)T=BTAT
La transposée du produit de deux matrices est le produit des transposées de chacune des matrices dans le sens inverse.
Exemple 6
Considérons l’exemple suivant:

Multiplier deux matrices avant de transposer le résultat est équivalent à faire la multiplication des transposées de chacune des matrices dans l’ordre inverse. Une fois de plus, utiliser ce résultat lors de vos simplifications algébriques.
Vous trouverez comment faire la multiplication de matrice dans la série de cours sur l’algèbre linéaire.
Exercices
Ceci est une série d’exercices résumant l’ensemble des enseignements étudiés dans ce cours. Vous trouverez la solution pour chacun de ces problèmes dans la section du solutionnaire.
Vous pouvez aussi utiliser cet outil pour effectuer vos calculs.
Exercice 1
Refaire tous les exemples dans le cours et valider vos réponses.
Solutions
Solution exercice 1
Voir les exemples dans le cours pour valider vos réponses.
FAQ sur la transposée d’une matrice
La transposée de matrice sert dans les calculs d’algèbre linéaire et d’algèbre vectorielle. La transposition de matrices est beaucoup utilisée dans des programmes informatiques( algorithmes) pour résoudre des systèmes d’équations linéaires rencontrés dans les problèmes d’ingénierie.
Pour transposer une matrice, il suffit de transformer toutes les lignes de la matrice en colonne. D’un autre point de vue, la transposée d’une matrice revient à transformer toutes les colonnes de la matrice en ligne.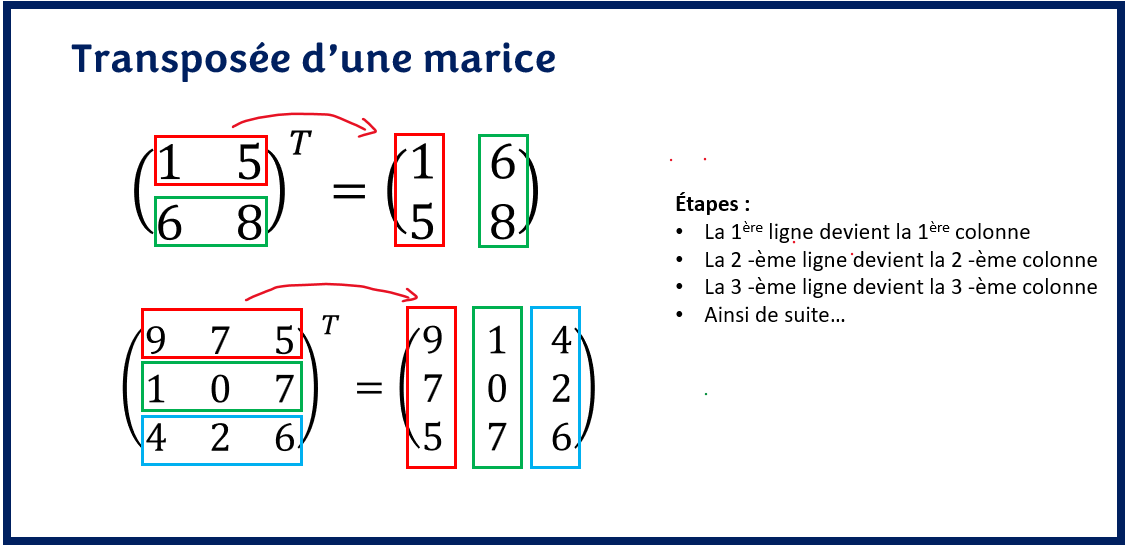
Oui, nous pouvons transposer des matrices rectangulaires. La transposée d’une matrice est toujours possible peut importe la dimension de la matrice. On transforme toujours toutes les lignes de la matrice en colonne ou alors on transforme toutes les colonnes en lignes. 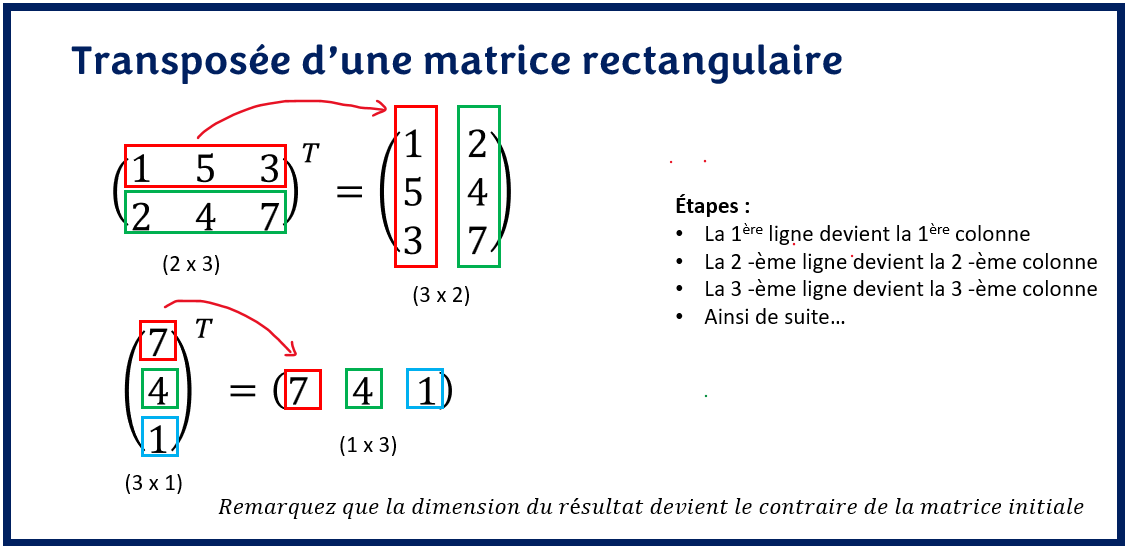
Pour faire la transposée du produit de deux matrices, on peut d’abord multiplier les deux matrices ensemble et ensuite faire la transposée du résultat obtenu. On peut aussi utiliser la propriété de la transposée de la multiplication de matrice : (AB)T=BTAT. La transposée du produit de deux matrices est le produit des transposées de chacune des matrices dans le sens inverse.
La transposée de la somme de deux matrices est tout simplement la somme des résultats de la transposée de chacune des matrices. En d’autres termes, on transpose d’abord chaque matrice, ensuite on additionne les résultats. Ceci est une propriété de la transposée de l’addition de matrices : (A+B)T=AT+BT
Si on transpose successivement deux fois la même matrice, on obtient encore la même matrice initiale. C’est comme si la deuxième transposée avait annulé la première transposée. C’est l’une des propriétés de la transposée de matrice : (AT)T= A
Pour transposer la multiplication d’une matrice par un scalaire, on transpose d’abord la matrice ensuite on la multiplie par le scalaire. On peut aussi multiplier la matrice par le scalaire avant de transposer le résultat. Tout ceci est possible grâce à cette propriété : (αA)T=α.AT
Sujets similaires
Vous pouvez aussi consulter les articles ci-dessous:
- OPÉRATIONS SUR LES MATRICESL’objectif est de présenter les opérations de bases sur les matrices : addition, soustraction, multiplication, transposé, déterminant et inverse à partir d’exercices résolus.
- COMMENT MULTIPLIER DES MATRICES?Vous trouverez les étapes nécessaires et suffisantes sur comment multiplier des matrices avec des exemples pratiques.
- COMMENT TRANSPOSER UNE MATRICE?Vous trouverez les étapes nécessaires et suffisantes sur comment transposer une matrice avec des exemples pratiques.
- TRANSPOSÉE D’UNE MATRICEL’objectif est d’apprendre à faire la transposée d’une matrice et découvrir les propriétés relatives à la transposition de matrice avec des exercices résolus.