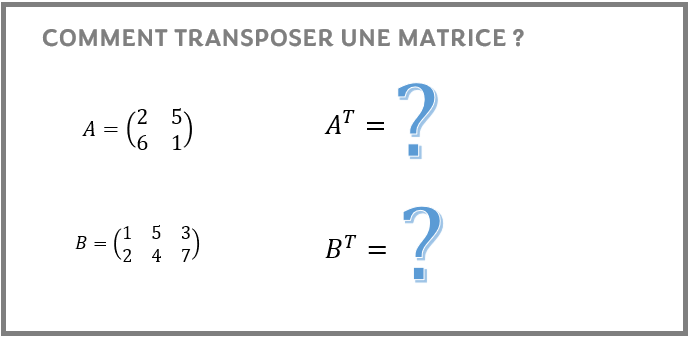
Vous trouverez les étapes nécessaires et suffisantes sur comment transposer une matrice avec des exemples pratiques.
Time needed: 6 minutes
Transposer une matrice est l’une des opérations sur les matrices que nous pouvons effectuer. De même que l’addition des matrices, la soustraction de matrice ou la multiplication de matrice, la transposée d’une matrice est très utile pour diverses situations en algèbre linéaire. La transposée d’une matrice est une opération simple de permutation des lignes et des colonnes de la matrice. Elle a de nombreuses propriétés que nous présentons dans l’article sur la transposée d’une matrice.
- Écrire la matrice à transposer
Toute matrice peut être transposée, quelle que soit sa dimension. La dimension d’une matrice est le nombre de lignes et de colonnes de la matrice. On parle aussi souvent de taille de la matrice ou ordre de la matrice. Puisque la transposée des matrices carrées permet d’obtenir une matrice de même dimension, nous commencerons par présenter la transposée de ce type de matrice.
Considérons deux exemples de matrices carrées:
– Une matrice A de dimension 2×2
– Une matrice B de dimension 3×3
- Préparer les cases de la matrice transposée
Transposer une matrice consiste à transformer les lignes de la matrice en colonne. Ainsi, on peut donc anticiper la dimension de la matrice transposée. La transposée d’une matrice carrée est une matrice carrée puisqu’elle a le même nombre de lignes et de colonnes. Le symbole de la transposée est: T (en exposant).
Dans notre exemple, la transposée des matrices A et B sera donc notée AT et BT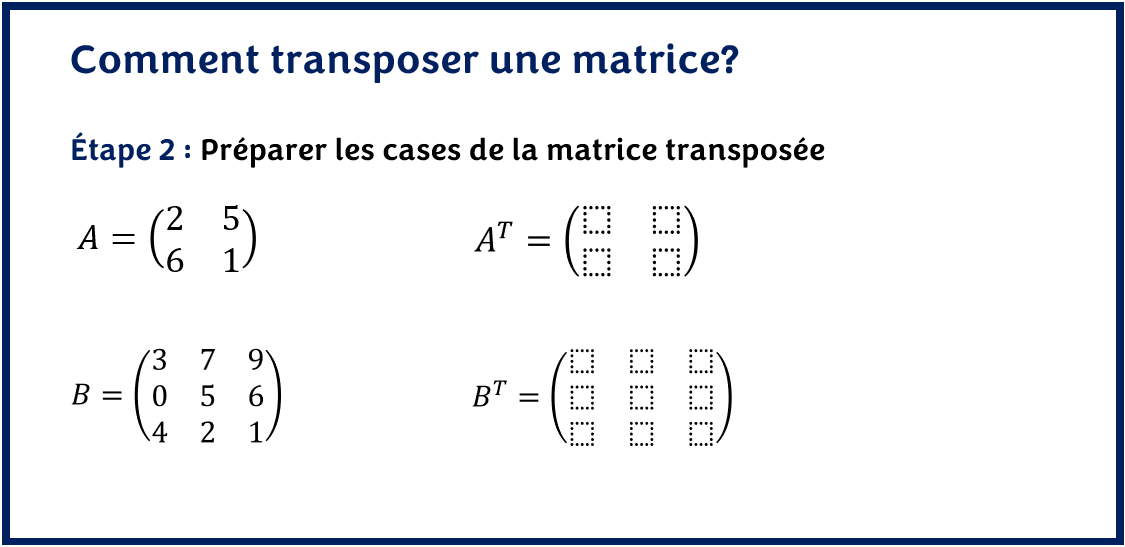
- Transformer les lignes de la matrice en colonnes
Chaque ligne de la matrice devient la colonne de la nouvelle matrice. Par exemple, la première ligne devient la première colonne, la deuxième ligne devient la deuxième colonne, ainsi de suite. C’est comme si, pour chaque ligne de la matrice, on faisait une rotation de 90 degrés dans le sens horaire.
On obtient donc une nouvelle matrice qui est appelée transposée de la matrice.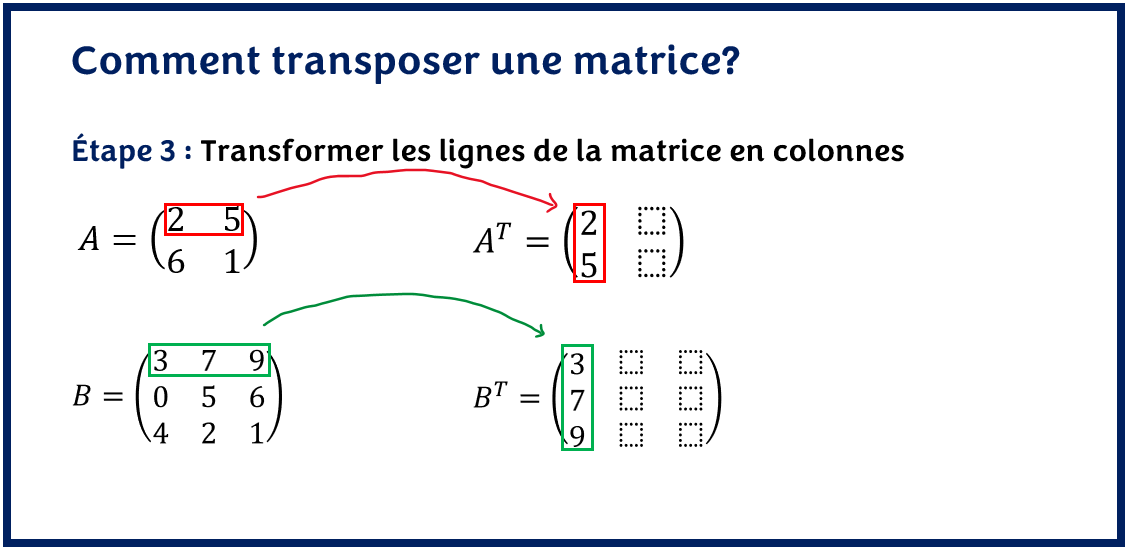
- Continuer la transformation avec les autres lignes de la matrice
La deuxième ligne devient la deuxième colonne de la matrice transposée. On continue ainsi autant de fois qu’il a de lignes dans la matrice.
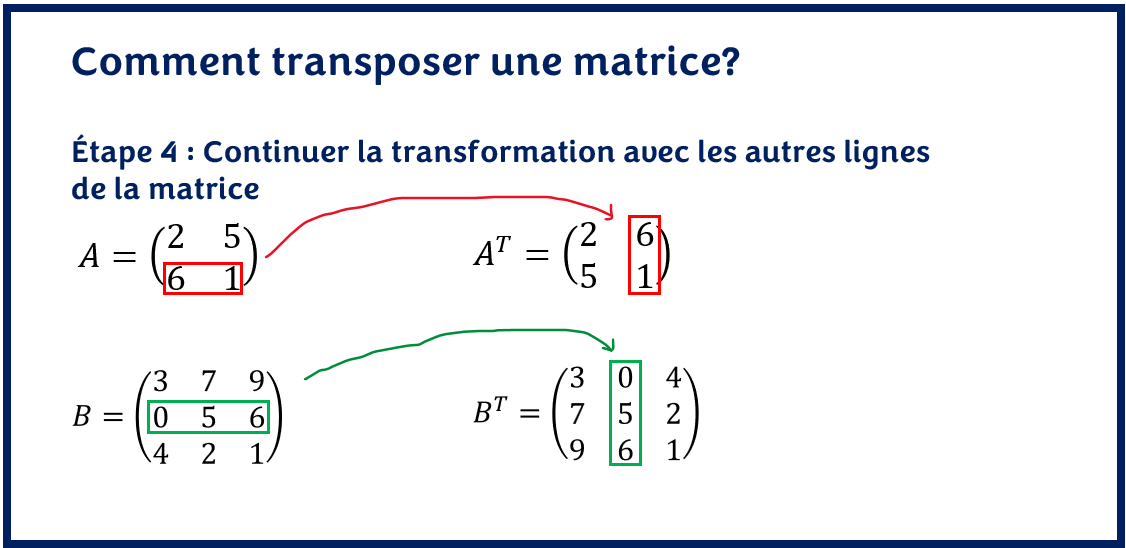
- Vérifier votre résultat
Même si la transposée est une opération simple, on peut quelquefois se tromper. Il est donc important de trouver un moyen de se vérifier rapidement en un clin d’oeil. C’est pourquoi on conseille de rapidement valider que les coefficients de la diagonale principale de la matrice transposée sont restés inchangés (à la même position). En effet, les coefficients de la diagonale sont les coefficients aii qui sont chacun à la même ligne et même colonne. Ainsi, la transformation de ligne en colonne ne les affecte donc pas.
Dans notre exemple, remarquez bien que les éléments de la diagonale des matrices A et B n’ont pas changé de position d’une matrice à l’autre.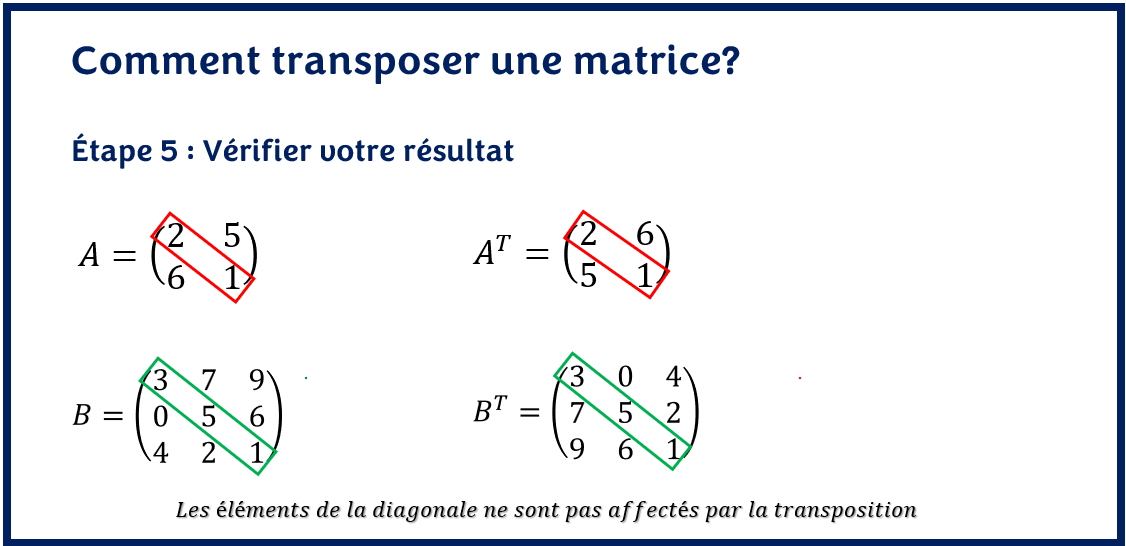
- Pratiquez-vous avec des matrices rectangulaires
Les matrices rectangulaires se sont des matrices dont le nombre de lignes est différent du nombre de colonnes dont des matrices de dimension n x m avec n le nombre de lignes et m le nombre de colonnes.
Puisque la transposition permute ou inverse les lignes en colonnes, alors si une matrice est de dimension n x m alors sa transposée sera de dimension m x n.
Le principe de transposition pour les matrices rectangulaires est exactement le même que pour les matrices carrées:
Étape 1: Écrire les matrices à transposer
Étape 2: Préparer les cases de la matrice transposée
N’oubliez pas de changer le nombre de ligne et de colonne. Par exemple, si la matrice A est de dimension 2 x 3, sa transposée AT sera de dimension de dimension 3 x 2. Donc, on devra plutôt préparer une matrice pour le résultat de trois lignes et deux colonnes.
Étape 3: Transformer les lignes de la matrice en colonne
Étape 4: Continuer la transformation de ligne jusqu’à la dernière
Étape 5:Vérifier votre résultat
Les matrices rectangulaires n’ont pas de diagonale principale, car elles ne sont pas carrées. Pour se vérifier, on s’assurera quand même que les coefficients qui ont le même numéro de ligne et de colonne n’ont pas changé.
On valide également la dimension de la matrice transposée puisqu’elle doit être différente de la matrice initiale.
Vous pouvez regarder une vidéo sur la transposée d’une matrice rectangulaire.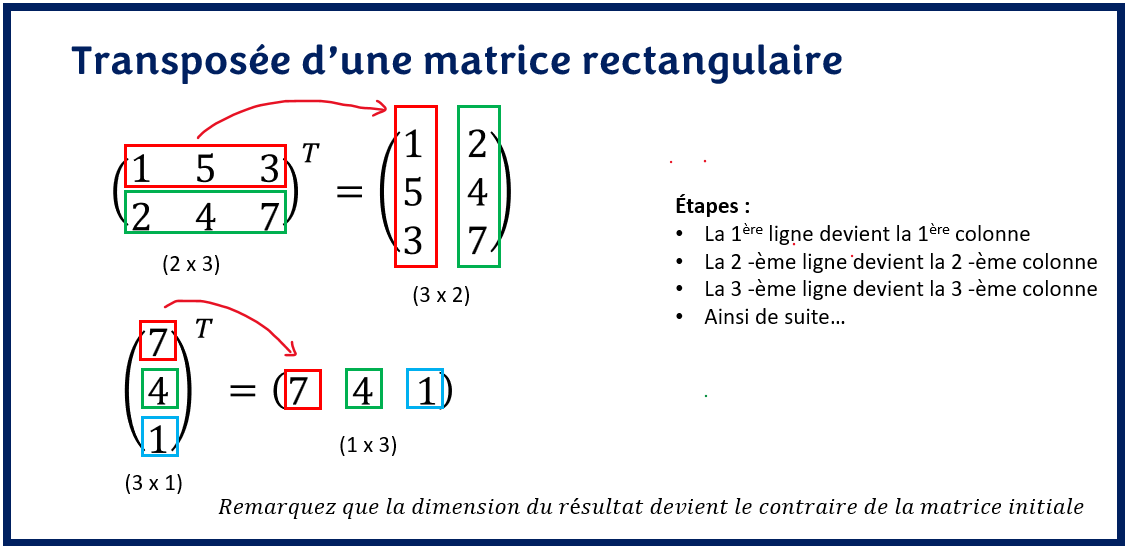
Conseils et astuces sur comment transposer une matrice
- La transposée d’une matrice existe, peu importe la dimension ou la taille de la matrice
- La transposée d’une matrice aussi souvent : tA, At ou AT
- On parle de transposée d’une matrice ou de transposition d’une matrice
- Pour transposer une matrice, on peut aussi transformer toutes les colonnes de la matrice en ligne
- Il ne faut pas oublier de vérifier rapidement son travail après avoir transposé, en validant la dimension de la matrice et en s’assurant que les éléments de la diagonale sont inchangés : si A est de dimension n x m alors AT sera de dimension m x n.
- La transposition de matrice obéit à plusieurs propriétés présentées dans un autre article.
Sujets similaires
- OPÉRATIONS SUR LES MATRICESL’objectif est de présenter les opérations de bases sur les matrices : addition, soustraction, multiplication, transposé, déterminant et inverse à partir d’exercices résolus.
- COMMENT MULTIPLIER DES MATRICES?Vous trouverez les étapes nécessaires et suffisantes sur comment multiplier des matrices avec des exemples pratiques.
- COMMENT TRANSPOSER UNE MATRICE?Vous trouverez les étapes nécessaires et suffisantes sur comment transposer une matrice avec des exemples pratiques.
- TRANSPOSÉE D’UNE MATRICEL’objectif est d’apprendre à faire la transposée d’une matrice et découvrir les propriétés relatives à la transposition de matrice avec des exercices résolus.