L’objectif est de présenter les opérations de bases sur les matrices : addition, soustraction, multiplication, transposée, inverse, déterminant à partir d’exercices résolus.
Sommaire
Rappel et mise en contexte
Les matrices sont d’une importance capitale dans le domaine de l’algèbre linéaire et facilitent grandement les calculs en ingénierie. Une matrice peut prendre plusieurs formes (carré ou rectangulaire) avec des caractéristiques différentes et des propriétés particulières. Les types de matrices particulières ont déjà été présentés dans le cours sur le langage matriciel.
Cet article fait suite à ce cours et récapitule l’ensemble des opérations de base sur les matrices. Il est donc important de savoir réaliser à la main ces opérations usuelles de bases à savoir : l’addition de matrices, la soustraction de matrices, la multiplication de matrices, la transposée d’une matrice, l’inverse d’une matrice et le déterminant d’une matrice.
Opérations sur les matrices: addition des matrices
L’addition est l’une des opérations sur les matrices les plus simples. Pour additionner deux matrices, il faut additionner les coefficients (les chiffres) de chaque matrice qui se trouvent à la même ligne et la colonne.
Considérons les exemples suivants :

En suivant la règle ci-dessous, on peut additionner un nombre infini de matrices. Le résultat de l’addition de deux matrices ou plusieurs matrices est une matrice de même taille que les autres matrices. On comprend donc qu’on ne peut donc pas additionner des matrices qui n’ont pas la même taille. Pour plus de détails, regarder l’exemple sur les conditions d’addition des matrices.
Opérations sur les matrices: soustraction des matrices
La soustraction de matrice est semblable à l’addition dans ce sens que c’est la même règle de calcul. Pour soustraire des matrices, on soustrait les coefficients des matrices situées à la même position de ligne et de colonnes.
Considérons les exemples suivants:

En suivant la même règle précédemment, on peut simultanément soustraire plusieurs matrices. Le résultat obtenu de la soustraction des matrices est une matrice de même taille que les autres. On ne peut pas soustraire des matrices qui n’ont pas la même taille. Pour plus d’informations, vous pouvez consulter le cours complet sur la soustraction de matrices.
Opérations sur les matrices: multiplication des matrices
Multiplication d’une matrice par un scalaire
Pour multiplier une matrice par un scalaire, il faut multiplier le scalaire par tous les éléments de la matrice. La dimension de la matrice n’a pas d’importance dans ce cas.
Considérons les exemples suivants :

Le résultat de la multiplication d’une matrice par un scalaire est une matrice de la même taille que la matrice initiale.
Multiplication des matrices
La multiplication des matrices est sans doute l’une des opérations sur les matrices les plus complexes à réaliser. Pour multiplier deux matrices, il faut calculer les coefficients (aij) de la matrice de résultat en multipliant chaque ligne i de la première matrice par chaque colonne j de la seconde matrice. Vous pouvez consulter l’article comment multiplier des matrices étape par étape.
Considérons l’exemple suivant :

La multiplication des matrices n’est pas toujours possible. En effet, il faut d’abord vérifier que les matrices sont compatibles c’est-à-dire que le nombre de colonnes de la première matrice doit être égal au nombre de ligne de la seconde.
On ne peut pas multiplier plusieurs matrices simultanément. On est obligé de faire la multiplication de matrices deux à deux jusqu’à obtenir le résultat final.
Le produit de matrice AB n’est pas toujours égal au produit BA car, les deux produits de matrices ne sont pas forcément compatibles. Le produit AB est égal au produit BA si les deux matrices sont inverses l’une de l’autre.
La multiplication des matrices n’est pas commutative c’est-à-dire que ABC ≠ BAC ≠ BCA ≠ CBA ≠ ACB ≠ CAB
Opérations sur les matrices: transposée d’une matrice
Parmi les opérations sur les matrices, la transposée est l’une des plus simples. Pour transposer une matrice, il faut transformer toutes les lignes de la matrice en colonne ou alors transformer toutes les colonnes de la matrice en ligne. Vous pouvez consulter l’article comment transposer une matrice étape par étape.
Considérons l’exemple suivant :
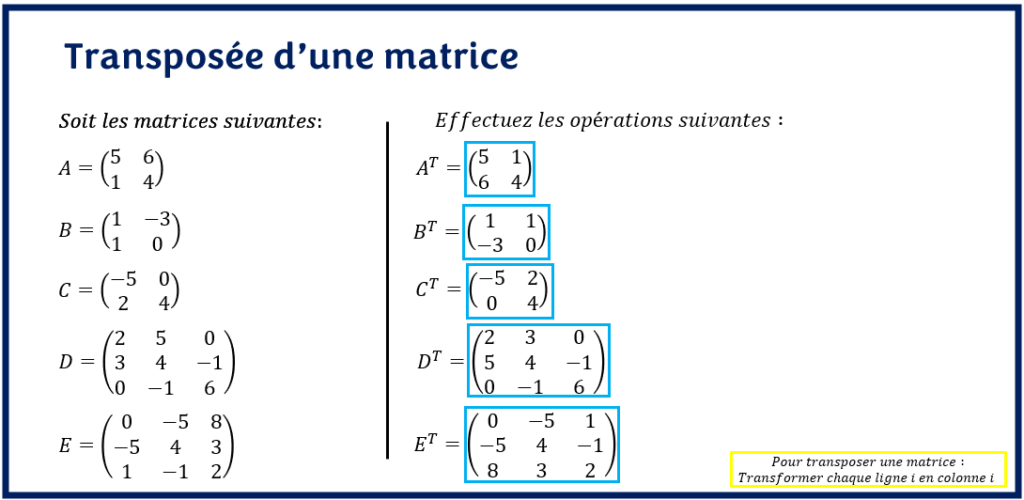
Lorsqu’on transpose une matrice, la diagonale est inchangée puisque les coefficients de la diagonale sont aii. Plus d’informations se trouvent dans le cours sur de la transposée d’une matrice.
Opérations sur les matrices: déterminant d’une matrice
Le calcul du déterminant d’une matrice sans aucun la doute notion la plus importe sur les matrices, car elle permet de créer des liens en plusieurs concepts d’algèbre linéaire.
Déterminant d’une matrice 2×2
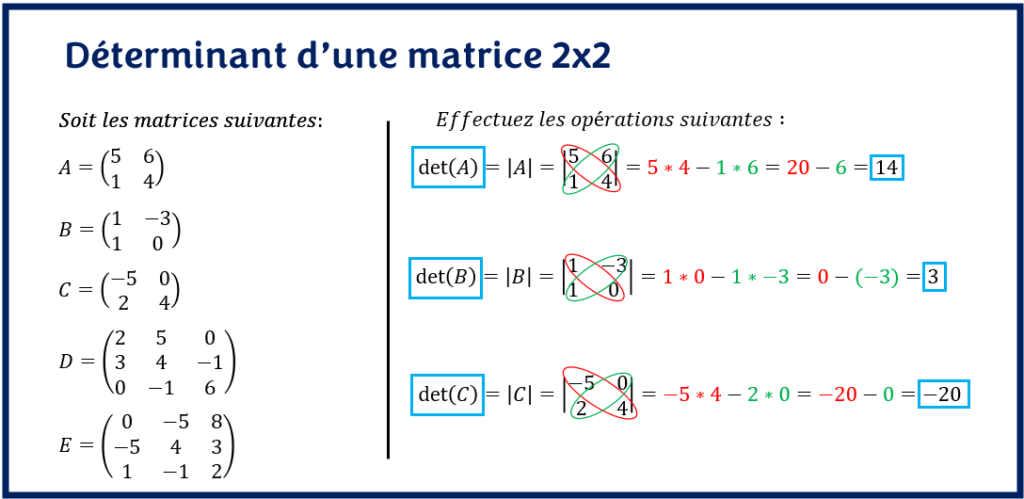
Pour calculer le déterminant d’une matrice 2×2, il faut utiliser la formule du déterminant d’une matrice 2×2.
Considérons l’exemple suivant:
Déterminant d’une matrice 3×3
Il existe plusieurs méthodes pour calculer le déterminant de matrice 3×3 ou plus. Parmi lesquels, le calcul du déterminant par la méthode élimination de GAUSS, le calcul du déterminant par la méthode d’expansion de cofacteur, le calcul du déterminant par la règle de Sarrus ou même le calcul du déterminant en utilisant les propriétés du déterminant d’une matrice.
Dans le cours sur le déterminant d’une matrice, nous avions présenté une astuce simple pour calculer rapidement le déterminant d’une matrice 3×3. C’est cette astuce que nous allons utiliser dans les exemples ci-dessous.
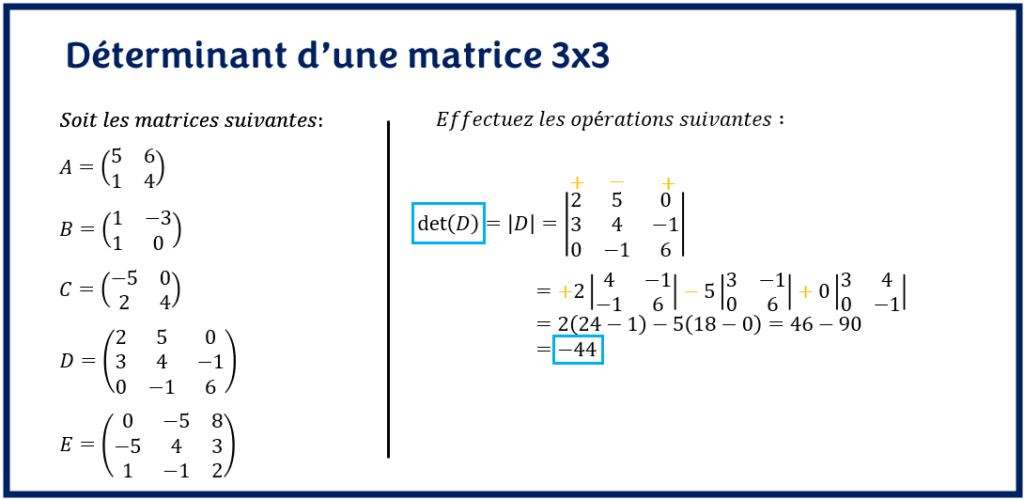
Vous pouvez consulter l’article comment calculer le déterminant d’une matrice 3×3 étape par étape.
Déterminant d’une matrice nxn
Le déterminant d’une matrice nxn se calcule en utilisant la même technique que celle d’une matrice 3×3 ou d’une matrice 4×4.
Opérations sur les matrices: inverse d’une matrice
L’une des dernières opérations sur les matrices est l’inverse d’une matrice. Elle est aussi importante que le déterminant d’une matrice. Également, il existe plusieurs méthodes pour calculer l’inverse d’une matrice. Entre autres, le calcul de l’inverse par la matrice adjointe, le calcul de l’inverse par l’élimination de GAUSS-JORDAN et le calcul de l’inverse avec les matrices élémentaires.
Inverse d’une matrice 2×2
Pour calculer l’inverse d’une matrice 2×2, il faut utiliser la formule de l’inverse d’une matrice 2×2.
Considérons l’exemple suivant :

Après le calcul de l’inverse d’une matrice, on peut vérifier le résultat en vérifiant l’égalité suivante : A*A-1 = In ou A-1*A = In.
Inverse d’une matrice 3×3
Pour calculer l’inverse d’une matrice 3×3, il faut utiliser la formule générale du calcul de l’inverse d’une matrice en utilisant la matrice adjointe.
Formule de l’inverse d’une matrice 3×3 ou nxn

Comatrice
Le calcul de la comatrice ou matrice des cofacteurs est une étape préliminaire pour le calcul de l’inverse d’une matrice. Vous pouvez consulter cette section pour savoir comment calculer la comatrice ou matrice des cofacteurs. La comatrice se note com(A).
Matrice adjointe
La matrice adjointe est la transposée de la comatrice aussi appelée matrice des cofacteurs. Le calcul de la transposée d’une matrice a présenté ci-dessus. L’adjointe d’une matrice se note Adj(A).
Calcul de l’inverse d’une matrice 3×3
L’inverse d’une matrice est trivial lorsqu’on sait calculer la matrice adjointe. Il suffit d’appliquer la formule de l’inverse d’une matrice 3×3 présentée ci-dessus.

Inverse d’une matrice nxn
L’inverse d’une matrice nxn se calcule en la même que celle d’une matrice 3×3. La formule a déjà été présentée ci-dessus.
Conseils et astuces concernant les opérations sur les matrices
- On peut additionner ou soustraire simultanément plusieurs matrices
- L’ordre dans lequel on calcule la somme des matrices ou la soustraction des matrices n’est pas important.
- On ne peut qu’additionner ou soustraire les matrices qui sont de la même dimension
- On ne peut pas multiplier simultanément plusieurs matrices. On les multiplie deux à deux.
- La multiplication de matrices n’est pas toujours possible. Il faut d’abord vérifier si elles sont compatibles.
- L’ordre selon lequel on dispose les matrices pour les multiplier est important
- Le produit de matrices AB n’est pas toujours égal au produit de matrices BA. Il est égal si les deux matrices sont inverses l’une de l’autre.
- La transposée d’une matrice laisse la diagonale de la matrice inchangée.
- La transposée change la dimension de la matrice. Si la matrice est de dimension nxm alors sa transposée est de dimension mxn.
- Le déterminant d’une matrice est nul si la matrice contient une ligne de zéro ou une colonne de zéro.
- Si le déterminant d’une matrice est nul, alors la matrice n’est pas inversible. Donc, on ne peut pas calculer A-1
- L’adjointe d’une matrice est la transposée de sa comatrice.
- L’inverse d’une matrice existe si son déterminant est non nul
- Vous pouvez utiliser ce logiciel pour effectuer vos calculs sur les matrices.
- Contactez-nous si vous avez toujours de questions.
FAQ concernant les opérations sur les matrices
Il existe plusieurs types de matrices parmi lesquels : matrice ligne, matrice colonne, matrice carrée, matrice rectangulaire, matrice triangulaire inférieure, matrice triangulaire supérieure, matrice symétrique, matrice antisymétrique, matrice nulle, matrice identité, matrice nulle, matrice idempotente, matrice nilpotente. Vous pouvez retrouver la définition et les exemples de ces matrices dans le cours sur le langage matriciel.
Plusieurs opérations peuvent être réalisées avec les matrices. Les opérations sur les matrices sont: l’addition, la soustraction, la multiplication, la transposée, le déterminant et l’inverse.
Pour calculer le produit de 3 matrices ABC, il faut calculer le produit des matrices deux à deux. On commence par calculer le produit BC ensuite on calcule le produit de A par le résultat du produit BC : ABC = A(BC). Consulter ce cours pour plus d’information.
La condition pour multiplier deux matrices est que les deux matrices sont compatibles c’est-à-dire que le nombre de colonnes de la première matrice (celle à gauche) est égal au nombre de ligne de la deuxième matrice (celle à droite). 
Pour calculer l’inverse d’une matrice 2×2, il faut permuter les deux éléments sur la diagonale de la matrice, ensuite attribuer un signe moins aux deux autres chiffres (chiffre sur l’antidiagonale) et enfin diviser tous les chiffres par le déterminant de la matrice.
Pour calculer l’inverse d’une matrice 3×3 ou l’inverse d’une matrice nxn, on utilise la formule de l’inverse d’une matrice ci-dessous.
Une matrice est inversible si le déterminant de la matrice est non nul. Une matrice est non inversible si le déterminant de la matrice est nul.
Sujets similaires
- OPÉRATIONS SUR LES MATRICESL’objectif est de présenter les opérations de bases sur les matrices : addition, soustraction, multiplication, transposé, déterminant et inverse à partir d’exercices résolus.
- COMMENT MULTIPLIER DES MATRICES?Vous trouverez les étapes nécessaires et suffisantes sur comment multiplier des matrices avec des exemples pratiques.
- COMMENT TRANSPOSER UNE MATRICE?Vous trouverez les étapes nécessaires et suffisantes sur comment transposer une matrice avec des exemples pratiques.
- TRANSPOSÉE D’UNE MATRICEL’objectif est d’apprendre à faire la transposée d’une matrice et découvrir les propriétés relatives à la transposition de matrice avec des exercices résolus.
- MULTIPLICATION DE MATRICEL’objectif est d’apprendre la multiplication de matrice et de présenter les propriétés relatives au produit matriciel avec des exercices résolus.
- SOUSTRACTION DE MATRICEL’objectif est d’apprendre à soustraire deux matrices ou plus et de présenter les propriétés relatives à la soustraction de matrice avec des exercices résolus.
- ADDITION DES MATRICESL’objectif est d’apprendre à additionner deux matrices ou plus et de présenter les propriétés relatives à l’addition des matrices avec des exercices résolus.
- MATRICES – LANGAGE MATRICIELL’objectif est d’introduire le concept des matrices à travers le langage matriciel par la définition de quelques matrices particulières et d’exercices résolus.