L’objectif est d’apprendre à additionner deux matrices ou plus et de présenter les propriétés relatives à l’addition des matrices avec des exercices résolus.
Sommaire
Addition de deux matrices
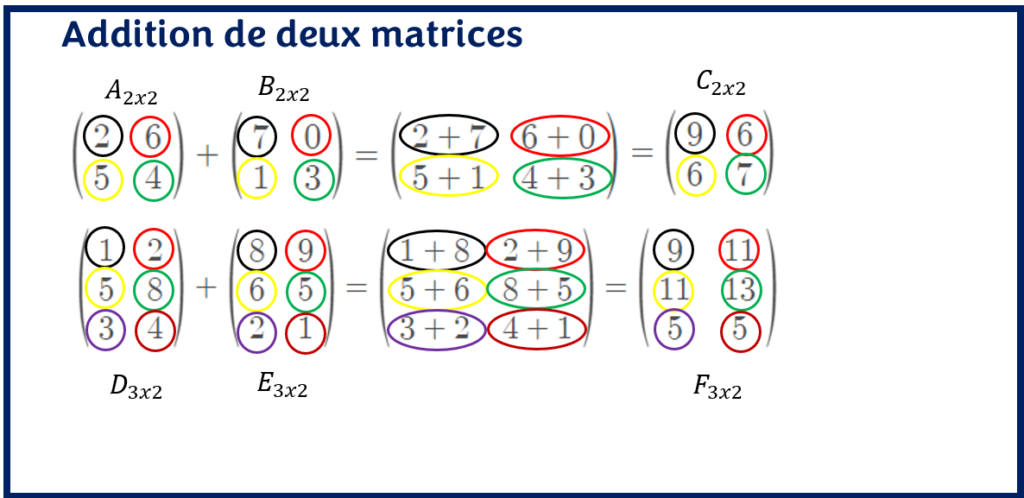
Additionner deux matrices revient à additionner les coefficients (les chiffres) de chaque matrice qui se trouvent sur la même ligne et la même colonne pour former une nouvelle matrice.
Il est donc nécessaire que les deux matrices aient la même taille (format) ou la même dimension. On peut donc additionner aussi bien des matrices carrées et des matrices rectangulaires. Vous pouvez consulter le cours sur le langage matriciel pour les définitions des matrices.
En ajoutant deux matrices, nous ajoutons les éléments de chaque ligne et colonne aux éléments respectifs de la ligne et de la colonne de la matrice suivante.
Additionner les matrices suivantes :
Note 1
On ne peut pas additionner deux matrices qui n’ont pas la même taille.
Dans chacun des cas suivants, dire si l’addition est possible

Addition de trois matrices ou plus
Additionner trois matrices ou plus revient à additionner les coefficients (les chiffres) de chaque matrice qui se trouvent sur la même ligne et la même colonne pour former une nouvelle matrice.
Il s’agit de la même technique que dans la section précédente. Il faut donc que toutes les matrices à additionner aient la même taille ou la même dimension.
Considérons les matrices A, B et C de dimension 2 x 2 ainsi que les matrices O, P, M et N de taille (3 x 1). Il est possible de les additionner simultanément comme dans l’exemple.
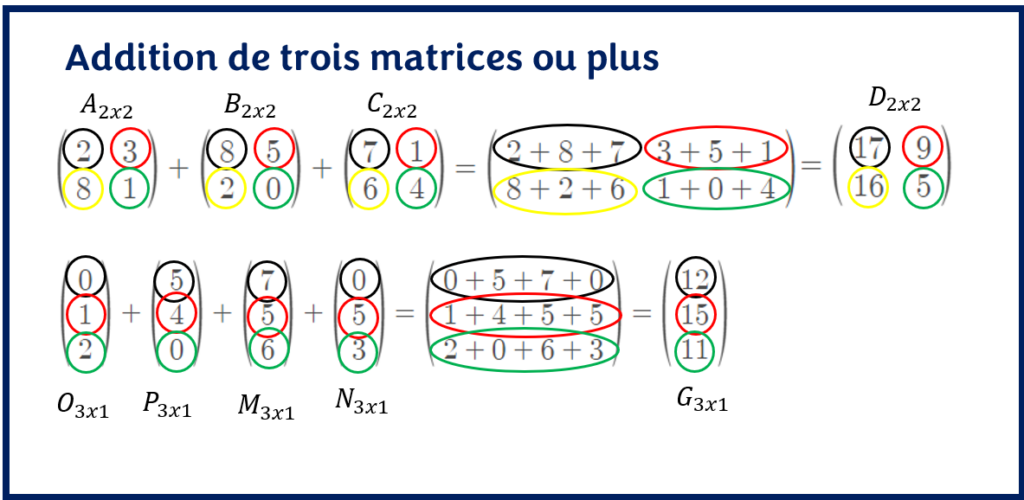
Dans le premier cas, on obtient comme résultat la matrice D qui est de même dimension que les matrices A, B et C. Similairement, dans le deuxième cas, la matrice G est aussi de même taille que les matrices O, P, M et N.
Note 2
Pour additionner simultanément trois ou plusieurs matrices, toutes les matrices doivent avoir la même taille.
Propriétés de l’addition des matrices
Tout comme l’ajout de nombres, l’ajout de matrice a également des propriétés similaires comme la commutativité, l’associativité, l’existence d’un élément inverse, l’existence d’un élément neutre, etc. La nécessité la plus importante pour l’ajout de matrices pour contenir toutes ces propriétés est que l’ajout de matrices est défini uniquement si l’ordre (la taille ou dimension) des matrices est le même.
Commutativité
Si A et B sont deux matrices d’ordre ( m x n ), alors A + B = B + A, c’est-à-dire que l’addition des matrices est commutative.
La commutativité signifie qu’on ne se soucie pas de l’ordre dans lequel les matrices sont additionnées.
Considérons l’addition des deux matrices suivantes :

On voit bien à travers cet exemple que la commutativité est vérifiée. Donc, A+B=B+A
Associativité
Si A, B et C sont trois matrices d’ordre ( m x n ), alors (A + B) + C = A + (B + C), c’est-à-dire que l’addition des matrices est associative.
En d’autres termes, si l’on doit additionner trois matrices ou plus, on peut les additionner progressivement par groupe de deux matrices. Une fois de plus, l’ordre dans lequel on additionne n’est pas pas important.
Considérons les trois matrices suivantes :

On voit bien à travers cet exemple que l’associativité est vérifiée. Malgré la différence des deux résultats en jaune, on obtient bien le même résultat final pour les deux cas. Donc (A+B)+C=A+(B+C)
Élément neutre
Si A est une matrice d’ordre ( m x n ), la matrice nulle O de taille ( m x n ) telle que A + O = O + A = A est l’élément neutre de l’addition des matrices.
En d’autres termes, le résultat de l’addition d’une matrice par l’élément neutre est la matrice elle-même
Considérons la matrice A suivante :

On voit bien à travers cet exemple que l’élément neutre existe. Donc, A+O=O+A=A.
Élément opposé
Si A est une matrice d’ordre ( n x m ), alors la matrice (-A) d’ordre ( n x m ) tel que A + (-A)=(-A) + (A) = O est l’élément opposé de la matrice A.
En d’autres termes, pour toute matrice A, il existe toujours une autre matrice (-A) pour laquelle la somme des deux matrices est nulle.
Considérons la matrice A de l’exemple 6

On voit bien à travers cet exemple que l’élément opposé existe. Donc, A + (-A)=(-A) + (A) = O.
Transposée
La transposée de la somme de deux matrices est égale à la somme des transposées des matrices respectives, c’est-à-dire ( A+ B) T = AT + BT.
En d’autre terme, la transposée de la somme c’est la somme des transposés.
Considérons l’exemple suivant:

Note 3
La transposée d’une matrice est la transformation des lignes de la matrice en colonne de la nouvelle matrice.
Conseils et astuces sur l’addition des matrices
- L’addition est définie uniquement si les matrices à additionner ont les mêmes dimensions ou le même ordre (même taille)
- L’addition de deux matrices ou plus s’obtient en additionnant les chiffres correspondants de chaque matrice
- L’addition obéit à plusieurs propriétés notamment la commutativité, l’associativité, etc
- L’addition est très similaire à la soustraction des matrices
Exercices
Ceci est une série d’exercices résumant l’ensemble des enseignements étudiés dans ce cours. Vous trouverez la solution pour chacun de ces problèmes dans la section du solutionnaire.
Vous pouvez aussi utiliser cet outil pour effectuer vos calculs.



Solutions
Vous trouverez ci-dessous la solution des exercices présentés à la section précédente

Consultez les astuces et les conseils au besoin

Solution exercice 1
Consulter l’addition de deux matrices ou de trois matrices au besoin

Consultez la section sur les propriétés de l’addition au besoin

Consultez la section sur les propriétés de l’addition au besoin

Consultez la section sur les propriétés de l’addition au besoin

Consultez les astuces et les conseils au besoin

Consultez les astuces et les conseils au besoin
Sujets similaires
- OPÉRATIONS SUR LES MATRICESL’objectif est de présenter les opérations de bases sur les matrices : addition, soustraction, multiplication, transposé, déterminant et inverse à partir d’exercices résolus.
- COMMENT MULTIPLIER DES MATRICES?Vous trouverez les étapes nécessaires et suffisantes sur comment multiplier des matrices avec des exemples pratiques.
- COMMENT TRANSPOSER UNE MATRICE?Vous trouverez les étapes nécessaires et suffisantes sur comment transposer une matrice avec des exemples pratiques.
- TRANSPOSÉE D’UNE MATRICEL’objectif est d’apprendre à faire la transposée d’une matrice et découvrir les propriétés relatives à la transposition de matrice avec des exercices résolus.