Vous apprendrez à calculer l’aire d’un carré et les propriétés relatives à un carré à partir d’exercices résolus.
Sommaire
Le carré est une figure géométrique à quatre côtés égaux. Il s’inscrit dans le grand groupe des quadrilatères. Un quadrilatère est une figure géométrique qui a quatre côtés. On peut citer par exemple, le carré, le rectangle, le parallélogramme, le losange, le trapèze, etc.
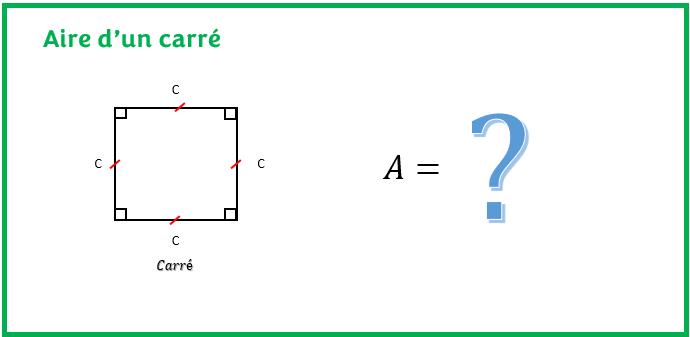
Aire d’un carré
L’aire ou la surface d’un carré est le produit d’un côté du carré par un autre. Étant donné, que le carré a tous ses côtés égaux, alors la formule de la surface d’un carré est aussi son carré exposant deux.
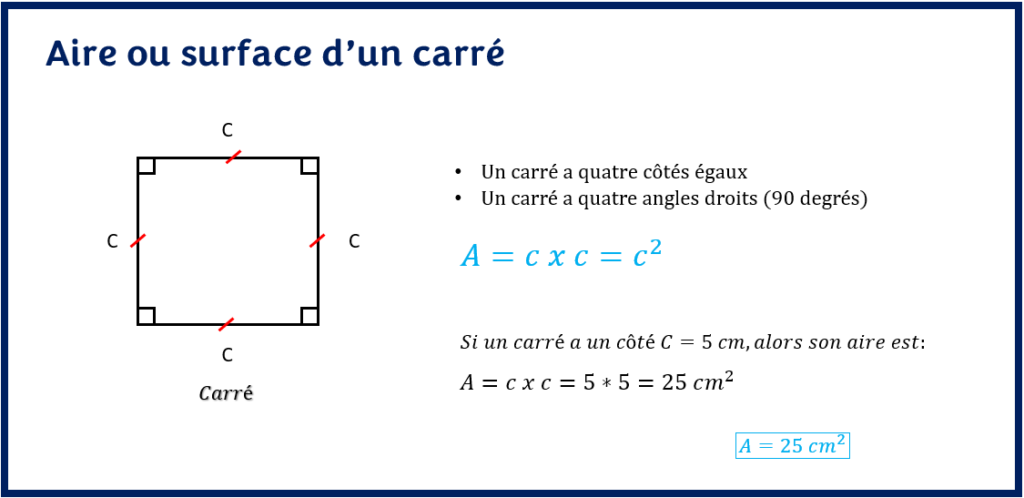
La surface d’un carré est un calcul simple. Il suffit simplement d’appliquer la formule. Quelquefois, il est nécessaire de convertir les unités pour la résolution de problème.
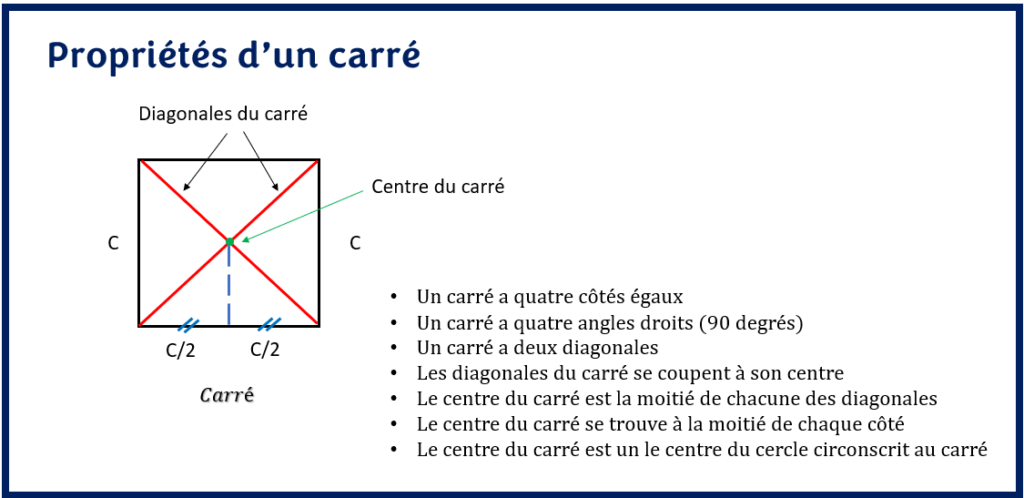
Propriétés d’un carré
- Un carré est une figure qui a quatre côtés égaux
- Un carré a toujours quatre angles de 90 degrés à chacun de ses sommets appelés angle droit.
- Un carré a deux diagonales
- Les diagonales d’un carré sont de la même longueur et se coupent au centre du carré
- le centre du carré est la moitié de chacune des diagonales
- Le centre du carré se trouve à la moitié de chaque côté
- Le centre du carré est le centre du cercle circonscrit au carré
Conseils et astuces concernant l’aire d’un carré
- Faites attention à la conversion d’unité dans le calcul de l’aire ou la surface d’un carré
- La longueur d’une diagonale d’un carré est de C√2 (côté du carré fois racine de deux). Nous démontrerons ce résultat dans le cours sur le théorème de Pythagore.
- Un carré est un quadrilatère
- Un quadrilatère est une figure à quatre côtés
- L’aire d’un carré est une mesure de la surface à l’intérieur du carré
- Les mesures manquantes pour le calcul d’aire du carré peuvent se calculer par la relation de Pythagore ou les relations métriques
- Pour construire le cercle circonscrit à un carré, il faut d’abord dessiner le centre du carré en traçant ses deux diagonales puis à l’aide d’un compas, dessiner le cercle circonscrit au carré en plaçant la pointe sur le centre du carré
- Consultez la vidéo explicative sur le calcul de l’aire d’un carré au besoin
Vidéo explicative de l’aire d’un carré
Vous pouvez consulter cette vidéo afin de mieux comprendre le calcul de l’aire d’un carré
Sujets similaires
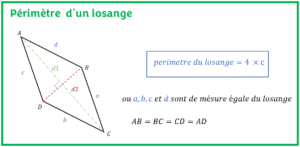
- Périmètre d’un losangeL’objectif est d’apprendre à calculer le périmètre d’un losange et de connaitre ses propriétés avec des exemples résolus.
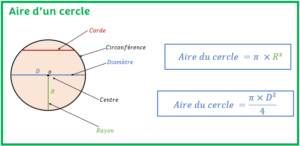
- Aire d’un cercleL’objectif est d’apprendre comment calculer l’aire d’un cercle et de connaitre ses propriétés avec des exemples résolus.
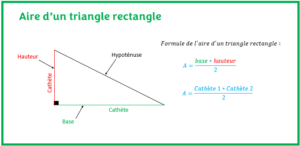
- Aire d’un triangle rectangleL’objectif est d’apprendre comment calculer l’aire d’un triangle rectangle de plusieurs façons différentes avec des exercices résolus.
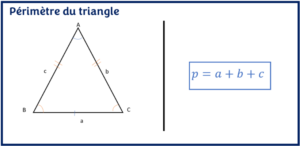
- Périmètre du triangleL’objectif est d’apprendre à calculer le périmètre du triangle et de connaître ses propriétés à partir d’exercices résolus.
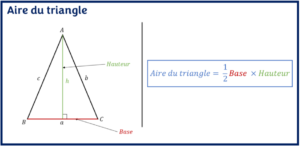
- Aire du triangleL’objectif est d’apprendre à calculer l’aire d’un triangle et de connaître ses propriétés à partir d’exercices résolus.
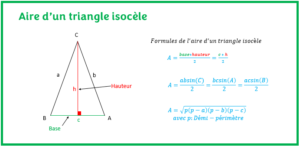
- Aire d’un triangle isocèleL’objectif est d’apprendre à calculer l’aire d’un triangle isocèle de plusieurs façons différentes avec des exercices résolus.
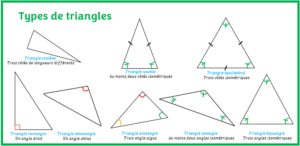
- Les types de trianglesL’objectif est d’apprendre les différents types de triangles existants et leurs propriétés avec des exemples résolus.
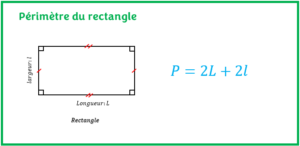
- Périmètre du rectangleL’objectif est d’apprendre à calculer le périmètre du rectangle et de connaître ses propriétés à partir d’exercices résolus.