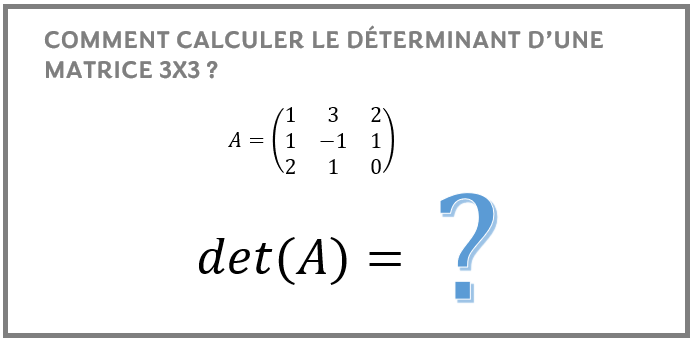Vous trouverez les étapes nécessaires et suffisantes sur comment calculer le déterminant d’une matrice 3×3 avec des exemples pratiques.
Time needed: 10 minutes
Une matrice est un tableau carré ou rectangulaire dans lequel sont disposés des éléments selon des lignes et des colonnes. Par ailleurs, de nombreuses opérations peuvent être réalisées sur les matrices : l’addition matricielle, la soustraction matricielle, la multiplication matricielle, la transposée d’une matrice et bien d’autres. En ce moment, nous allons voir comment nous pouvons calculer un déterminant sur une matrice 3×3. En algèbre linéaire, le déterminant d’une matrice est une notion très importante, car elle permet de savoir si la matrice est inversible, de vérifier si des vecteurs sont linéairement indépendants, de calculer les valeurs et les vecteurs propres d’une matrice. Vous pouvez consulter le calcul du déterminant de matrice 2×2 pour faciliter votre compréhension dans cette leçon.
- Poser le déterminant de la matrice si possible pour le calcul
On ne peut pas calculer le déterminant d’une matrice rectangulaire( matrices qui n’ont pas le même nombre de lignes et de colonnes). Pour une matrice carrée A de dimension (n x n), il est possible de calculer son déterminant. On note det (A) ou |A|.
Ici, le déterminant de la matrice A se pose comme suite:.
- Choisir la ligne ou la colonne à utiliser
Il est toujours préférable de choisir la ligne ou la colonne de la matrice avec le plus de zéro possible. Cela facilite les calculs étant donné que certaines opérations ne seront pas effectuées tout simplement.
Il est à noter que peu importe la ligne ou la colonne choisie, on obtiendra toujours le même résultat.
Dans notre exemple, pour le calcul du déterminant de la matrice A on a deux choix possibles:
– Choisir la troisième ligne de la matrice A : 2 1 0
– Choisir la troisième colonne de la matrice A : 2 1 0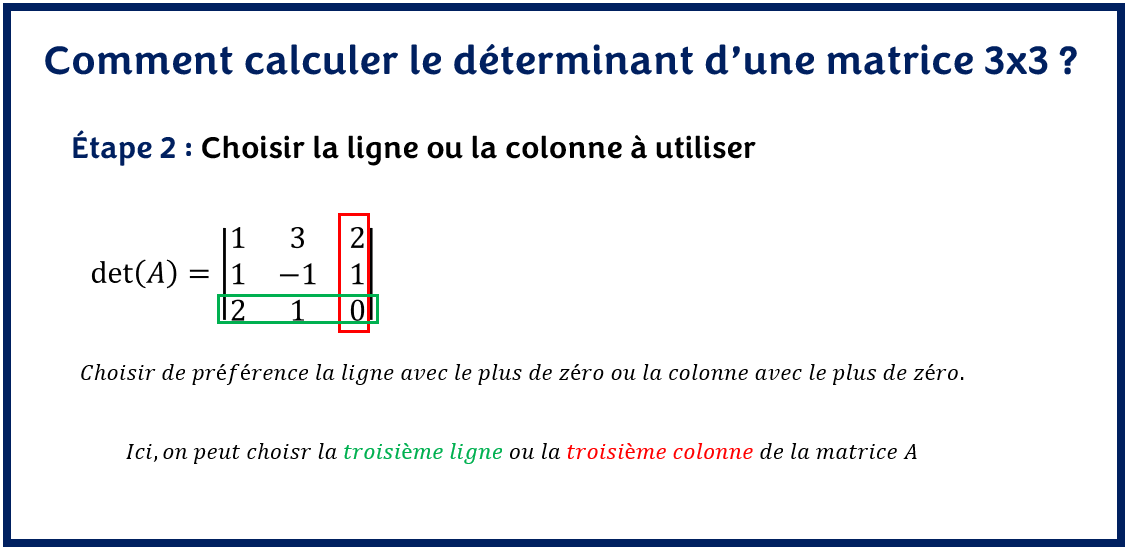
- Inscrire le signe des cofacteurs sur la ligne ou la colonne choisie
Inscrire au-dessus de chaque chiffre de la ligne ou de la colonne choisie le signe de son cofacteur correspondant. Nous présentons ici une astuce rapide qui permet de calculer le déterminant de la matrice sans utiliser la formule rigoureuse.
Le premier élément de la matrice (le coefficient a11) a toujours le signe plus (+). Tous les autres signes des cofacteurs des autres coefficients se déduisent en alternant successivement le signe donné au précédent.
- Barrer la ligne et la colonne du premier coefficient de la ligne ou de la colonne choisie
Prenez en considération le premier coefficient de la ligne ou de la colonne choisie. Barrez la ligne correspondante à ce coefficient d’un trait horizontal et barrez la colonne correspondante à ce coefficient d’un trait vertical. Il reste donc quatre coefficients non barrés qui forment une matrice 2×2.
Dans notre exemple, puisque nous avons sélectionné la troisième colonne alors :
– Le premier coefficient est a13=2
– On barre donc sa ligne d’un trait horizontal. On barre donc 1 3 2
– On barre aussi sa colonne d’un trait vertical. On barre donc 2 1 0
– Il reste donc une matrice 2×2
- Calculer le déterminant de la matrice 2×2 obtenu
Le déterminant d’une matrice 2×2 s’obtient en calculant la différence du produit croisée. C’est ainsi qu’on obtient le déterminant de la sous matrice 2×2 qui est appelé mineur M13 qui représente le déterminant de la matrice obtenu en barrant la première ligne et la troisième colonne.
Dans notre exemple, le déterminant de la matrice 2×2 obtenu est : M13 = (1 * 1) – (2 * (-1)) = 1 + 2 = 3.
- Multiplier le mineur par son coefficient avec le signe de son cofacteur
Multiplier le résultat du déterminant de la sous matrice 2×2 obtenu par le coefficient à l’intersection de la ligne et de la colonne barrée avec le signe de son cofacteur.
Dans notre exemple,
– Le déterminant de la sous matrice était : M13 = 3
– Le coefficient à l’intersection de la ligne et de la colonne barrée correspondant à ce mineur est : + 2 (ne pas oublier de le multiplier par le signe du cofacteur)
– On multiplie et on obtient : (3) * (+2) = 6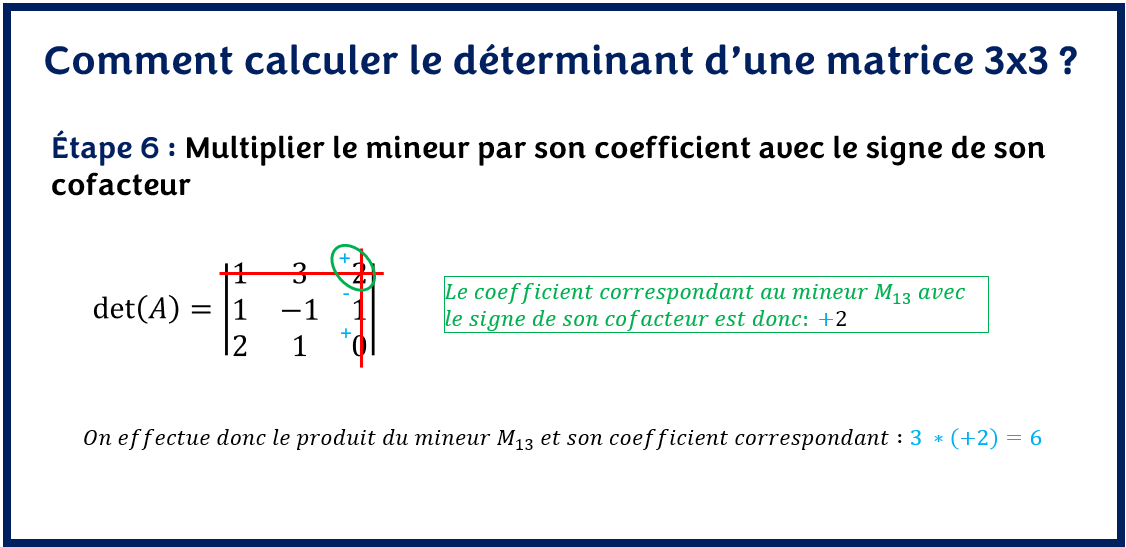
- Recommencer les étapes 4 à 6 avec le deuxième coefficient
Puisque le calcul du déterminant de la matrice est fait selon la troisième colonne alors on passe au deuxième coefficient. On commence donc par barrer sa ligne et sa colonne correspondante puis on calcule le déterminant de la sous matrice obtenue. Enfin, on multiplie ce déterminant par son coefficient correspondant en tenant compte du signe de son cofacteur.
Dans notre exemple:
– le deuxième coefficient est : a23 = 1
– On barre donc la deuxième ligne d’un trait horizontal : 1 -1 1
– On barre aussi la troisième colonne d’un trait vertical : 2 1 0
– On calcule le déterminant de la sous-matrice 2×2 obtenue: M23 = (1*1) – (2 * 3) = 1 – 6 = -5
– Le coefficient à l’intersection de la ligne et de la colonne barrée correspondant à ce mineur est : – 1 (ne pas oublier de le multiplier par le signe du cofacteur)
– On multiplie et on obtient : (-5) * (-1) = 5
- Terminer le calcul avec le troisième coefficient de l’étape 4 à 6
Étant donné que le troisième coefficient est nul (a33 = 0), il n’est pas nécessaire de faire un calcul puisqu’à la fin on doit le multiplier par le mineur M33. Le résultat sera donc toujours nul.
C’est justement la raison pour laquelle à l’étape 2, on demande de choisir la ligne ou la colonne contenant le plus de zéro pour le calcul du déterminant.

- Additionner les trois résultats obtenus (les cofacteurs)
La dernière étape pour calculer le déterminant de la matrice 3×3 est l’addition des résultats obtenus aux étapes 6, 7 et 8.
Dans notre exemple, on a donc: det(A) = 6 + 5 + 0 = 11.
- Calcul du déterminant sur une ligne.
Le calcul du déterminant de la matrice A peut se faire de façon plus compacte sur une seule ligne en respectant toutes les étapes présentées ci-dessus. Cette façon de faire est d’ailleurs celle conseillée puisque cela se présente bien sur une feuille de papier et occupe moins d’espace.

Conseils et astuces sur comment calculer le déterminant d’une matrice
- Le déterminant d’une matrice comportant une ligne complète de zéro ou une colonne complète de zéro est forcément nul.
- La méthode de calcul du déterminant d’une matrice 3×3 est la même que celle d’une matrice 4×4, 5×5 ou plus. Néanmoins, les calculs sont plus longs.
- Le déterminant d’une matrice rectangulaire n’existe pas
- Consultez la vidéo explicative sur comment calculer le déterminant d’une matrice 3×3.
- Effectuez vos calculs sur les matrices sur la plateforme de Symbolab pour vous vérifier rapidement.
Sujets similaires
- PROPRIÉTÉS DU DÉTERMINANT D’UNE MATRICEL’objectif est d’apprendre à utiliser les propriétés du déterminant d’une matrice afin de calculer le déterminant sans calculer la matrice
- INVERSE D’UNE MATRICEL’objectif est d’apprendre à calculer l’inverse d’une matrice et de découvrir les propriétés de l’inverse avec des exemples résolus.
- COMMENT CALCULER LE DÉTERMINANT D’UNE MATRICE 3×3?Vous trouverez les étapes nécessaires et suffisantes sur comment calculer le déterminant d’une matrice 3×3 avec des exemples pratiques.
- DÉTERMINANT D’UNE MATRICEL’objectif est d’apprendre à calculer le déterminant d’une matrice par la méthode d’expansion en cofacteurs avec des exercices résolus.