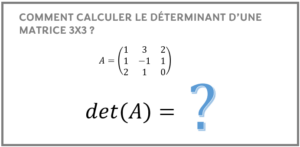L’objectif est d’apprendre à calculer l’inverse d’une matrice et de découvrir les propriétés de l’inverse avec des exemples résolus.
Sommaire
Rappel et mise en contexte
Une matrice est un tableau carré ou rectangulaire dans lequel des éléments sont disposés suivant des lignes et des colonnes. Il est donc nécessaire de savoir comment lire chacun des éléments du tableau appelés coefficients.
Plusieurs opérations sont réalisables sur les matrices: l’addition, la soustraction, la multiplication, le déterminant. Autant de possibilités qui ont chacune leurs particularités. Nous verrons que la notion de déterminant d’une matrice est intimement liée à la notion de l’inverse d’une matrice.
Il sera donc très important de créer des liens entre ces deux notions spécifiques d’ici la fin de ce cours. De ce fait, les notions de mineurs d’une matrice ou de cofacteurs d’une matrice sont à connaître.
Condition de l’existence de l’inverse d’une matrice
Toutes les matrices ne sont pas inversibles. En effet, une matrice carrée est inversible si et seulement si le déterminant de la matrice est différent de 0.
Inverse d’une matrice 2×2
L’inverse d’une matrice 2×2 est le plus simple des inverses. La formule permet d’obtenir le résultat en une seule opération si on connaît la valeur du déterminant.
L’inverse d’une matrice se note A-1 et vérifie l’équation selon laquelle AA-1 = A-1A = In.
Où, In est la matrice identité d’ordre n.
Une mnémotechnique pour retenir la configuration d’un inverse est de permuter les éléments sur la diagonale et de multiplier par moins les éléments sur l’anti-diagonale. Vous l’aurez remarqué, le calcul de l’inverse demande de savoir multiplier une matrice par un scalaire.
Vérification de l’inverse d’une matrice
Afin de vérifier son résultat, on peut valider que l’équation suivante est vraie: AA-1 = A-1A = In. Cette équation sert aussi à vérifier si une matrice B quelconque est l’inverse d’une matrice A. Dans ce cas, on vérifiera l’équation suivante : AB = BA = In.
Cette validation est aussi valable pour les matrices de dimension nxn. Bien sûr, si le produit de matrice n’est pas possible (Compatibilité des matrices), alors les deux matrices ne sont pas forcément l’inverse l’une de l’autre.
Inverse d’une matrice 3×3
Le calcul de l’inverse des matrices 3×3 est aussi assez simple comme celui des matrices 2×2. Il nécessite juste un plus de calcul puisque la matrice a plus de coefficients.
La première étape avant le calcul de l’inverse est le calcul du déterminant. Si la matrice a un déterminant nul, on s’arrête, car la matrice n’est pas inversible. Si la matrice a un déterminant non nul, on continue les calculs par la matrice des cofacteurs (9 coefficients à calculer) encore appelée comatrice.
Voici un exemple:
Calcul du déterminant de la matrice A
Vous pouvez consulter l’article sur comment calculer le déterminant d’une matrice 3×3 ou consulter le cours sur le déterminant d’une matrice.
Ici, calcul le déterminant de la matrice A en utilisant la troisième colonne de la matrice, car elle a le plus de zéro. Cela simplifie le calcul. Puisqu’on a trouvé un déterminant non nul, la matrice A est donc inversible.
Calcul de la matrice cofacteur de A
La matrice cofacteur de A se note coef(A). On avait déjà présenté comment calculer le cofacteur d’un élément d’une matrice. On rappelle que le cofacteur associé à une ligne i et une colonne j est donné par :
Le cofacteur Cij se défini à partir du mineur Mij par la relation: Cij= (-1)i+jMij. Dans les faits, on calculera différemment sans plus penser à la formule.
La matrice des cofacteurs de A se nomme aussi comatrice notée com(A).
En pratique, avant de calculer les cofacteurs de la matrice A, on commence par mettre le signe des cofacteurs sur la matrice. Le premier élément de la matrice a toujours le signe +. Les autres signes sont déduits en alternant les signes d’un chiffre à l’autre(+, –, +, –, +). Ensuite, on calcule le déterminant obtenu en barrant la ligne et la colonne correspondante. Ce résultat du déterminant sera donc multiplié par le signe du cofacteur. Finalement, on l’écrit dans la matrice coef(A) dans la position de la ligne et la colonne correspondante.
Calcul de la matrice adjointe de A
La matrice adjointe n’est rien d’autre que la matrice cofacteur de A transposé. Elle se note : Adj(A).
Pour transposer une matrice, on transforme les lignes de la matrice en colonne ou alors les colonnes de la matrice en lignes.
Calcul de l’inverse de la matrice A
On peut maintenant terminer le calcul puisqu’on a tout ce qu’il nous faut (déterminant et matrice adjointe).
Il n’est pas nécessaire de multiplier tous les éléments de la matrice adjointe par 1/15 puisque de toute façon, on obtient des fractions. Après le calcul de l’inverse, il est souvent utile de vérifier son résultat vérifiant l’une ou l’autre des équations suivantes : AA-1 = In ou A-1A = In. Ici, n=3, car, on a une matrice 3×3.
Inverse d’une matrice d’ordre n
L’inverse d’une matrice d’ordre n ou de dimension (n x n) est donné par la relation :
On suit exactement la même méthode que celle d’une matrice (3 x 3). On commence par le calcul du déterminant puis de l’adjointe.
Propriétés
Soit trois matrices A, B et C d’ordre n inversibles c’est-à-dire que le déterminant de chacune des matrices est différent de zéro (det(A)≠0, det(B)≠0, det(C)≠0).
Les propriétés suivantes sont vraies:
On peut donc formuler quelques remarques pour certaines propriétés:
- l’inverse est unique ce qui signifie qu’on ne peut pas avoir deux inverses différents pour une même matrice.
- La deuxième propriété peut être utilisée pour vérifier si la matrice qu’on a calculée est bien l’inverse de la matrice souhaitée.
- Les propriétés 3 et 4 sont surtout utilisées dans des démonstrations.
- La propriété 5 montre que l’inverse de la matrice identité est la matrice identité
- Les propriétés 5 et 6 montrent que l’inverse d’un produit de matrices est le produit des inverses de chacune des matrices dans le sens contraire d’apparition.
- La propriété 8 nous apprend qu’on peut permuter l’inverse et la transposer. En d’autres termes, on peut transposer une matrice avant de trouver son inverse ou plutôt on peut calculer d’abord l’inverse de la matrice avant de la transposer. Les deux façons de faire sont équivalentes.
- Quant à la propriété 10, elle nous apprend que le déterminant de l’inverse d’une matrice est l’inverse du déterminant de la matrice.
Conseils et astuces
- Avant de calculer l’inverse d’une matrice, il faut d’abord vérifier que son déterminant est différent de 0
- La formule de l’inverse des matrices d’ordre 2 ou d’ordre n doit être apprise par coeur
- La matrice des cofacteurs de A se nomme aussi comatrice notée com(A).
- La propriété 2 peut être utilisée pour valider le résultat
- Les propriétés 7, 8 et 10 sont super intéressantes dans des problèmes, car elles évitent de recommencer les calculs à zéro.
- Vous pouvez utiliser cette plateforme pour vérifier vos résultats rapidement.
- Vous pouvez consulter cette vidéo pour version audio.
FAQ sur l’inverse d’une matrice
C’est le cas, si son déterminant est différent de zéro. Dans ce cas, on dit que la matrice est inversible. Si le déterminant de la matrice i est égal à zéro, alors i n’a pas d’inverse. Dans ce cas, la matrice est singulière ou non inversible.
Avant de faire ce calcul, il faut d’abord vérifier que son déterminant est différent de zéro. Il existe plusieurs techniques pour le calcul: en utilisant la formule de la matrice adjacente, en utilisant l’élimination de Gauss-Jordan sur la matrice augmentée ou autres. Ci-dessous la formule utilisant la matrice adjacente. Elle est valide, peu importe la dimension de la matrice.
Pour le démontrer, il suffit de montrer que le produit de A par B donne l’identité ou l’inverse.
C’est-à-dire: AB = In ou BA =In
L’inverse d’une matrice matrice 2×2 peut se calculer utilisant la méthode de Gauss-Jordan sur la matrice augmentée [A ¦ I]. Mais, il est beaucoup plus facile et plus rapide d’utiliser directement la formule ci-dessous:
L’inverse d’un produit de matrices est tout simplement le produit de l’inverse de chacune des matrices dans le sens inverse: (AB)-1=B-1A-1
Il s’agit d’utiliser la propriété 6. Dans le cas où l’on a plus de deux matrices, on effectue toujours le produit des inverses dans le sens inverse. (propriété 7)
L’inverse d’une matrice transposée est simplement la transposée de l’inverse de la matrice. (AT)-1=(A-1)T. Il s’agit de la propriété 8.
Le déterminant de la matrice A-1 est simplement l’inverse de la valeur du déterminant de la matrice A c’est-à-dire : det(A-1)=1/det(A). Il s’agit de la propriété 10.
Sujets similaires
Vous pouvez aussi consulter :
- MÉTHODE DE GAUSS
L’objectif est d’apprendre à résoudre un système d’équations linéaires par la méthode de Gauss à partir d’exercices résolus. - MATRICE AUGMENTÉE
L’objectif est d’apprendre à écrire la matrice augmentée d’un système d’équations et de l’échelonner à l’aide d’exercices résolus. - MATRICES ÉCHELONNÉES
L’objectif est d’apprendre à échelonner une matrice et à reconnaître les matrices échelonnées à l’aide d’exercices résolus. - FORME AX=B : TRANSFORMER UN SYSTÈME D’ÉQUATIONS LINÉAIRES
L’objectif est d’apprendre comment transformer un système d’équations linéaires sous la forme AX=B avec des exercices résolus. - MÉTHODE PAR ÉLIMINATION
L’objectif est d’apprendre à résoudre un système d’équations linéaires par la méthode d’élimination avec des exercices résolus. - MÉTHODE DE SUBSTITUTION
L’objectif est d’apprendre à résoudre un système d’équations linéaires par la méthode de substitution avec des exercices résolus. - MÉTHODE DE COMPARAISON
L’objectif est d’apprendre à résoudre un système d’équations linéaires par la méthode de comparaison avec des exercices résolus. - SYSTÈME D’ÉQUATIONS LINÉAIRES
L’objectif est d’apprendre à reconnaître et déterminer l’ensemble de solution d’un système d’équations linéaires avec des exemples résolus.