Découvrez les trois types de solutions d’un système. Apprenez comment savoir si un système admet des solutions avec des exercices résolus.
Sommaire
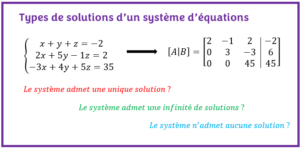
Les systèmes d’équations constituent l’élément essentiel de résolution des problèmes en algèbre linéaire. On distingue plusieurs techniques de résolution des systèmes d’équations. On peut citer : la méthode de comparaison, la méthode de substitution, la méthode d’élimination, la méthode de Gauss, la méthode de Gauss-Jordan et la méthode de la matrice inverse. Peu importe la méthode de résolution des systèmes d’équations utilisées, le système a toujours trois types de solutions :
- le système admet une solution unique
- le système admet une infinité de solution
- le système n’admet aucune solution
Cet article, vous livre tous les secrets pour identifier le type de solutions d’un système d’équations avant même de trouver son ensemble de solution. Les concepts préliminaires à cet article sont : le déterminant d’une matrice, l’inverse d’une matrice, le rang d’une matrice, le nombre de pivots d’une matrice, la matrice augmentée échelonnée.
Comment savoir si un système admet une solution? C’est la question à laquelle nous allons répondre dans cet article.
Comment savoir si un système admet une solution?
La première étape pour savoir si un système admet une solution est d’échelonner le système.
Considérons un système écrit sous la forme AX=B. En règle générale,
Si la matrice A est carrée, alors :
- Le système admet une solution unique si le déterminant de la matrice A est différent de zéro : det (A) ≠ 0
- le système admet une infinité de solution ou le système n’admet pas de solution si le déterminant de la matrice A est nulle ( det(A) = 0 ).
- le système d’admet pas de solution s’il n’admet pas une solution unique et s’il n’admet pas une infinité de solution
Si la matrice A est rectangulaire, alors :
- le système ne peut pas admettre une solution unique.
- le système admet une infinité de solutions ou le système n’admet pas de solution.
- Le système admet une infinité de solutions si le rang de la matrice A est égal au rang de la matrice augmentée [A|B]. En d’autres termes, le système admet une infinité de solutions la matrice A et la matrice augmentée [A|B] ont les mêmes pivots.
- Le système n’admet pas de solution s’il n’admet pas une infinité de solutions.
Comment savoir si un système admet une unique solution ?
Considérons un système d’équations écrit sous la forme AX=B.
Le système admet une unique solution ou une solution unique si :
- Le déterminant de la matrice A est non nul 0 : det (A) ≠ 0
- La matrice A a tous ses pivots : la matrice A est plein rang
- La matrice augmentée échelonnée [A|B] a tous tous ses pivots : la matrice augmentée est plein rang.
- La matrice A est inversible : la matrice inverse A-1 existe.
- La matrice A est carrée et le rang de la matrice A est égal au rang de la matrice augmentée [A|B]
- Les colonnes de la matrice A sont linéairement indépendantes : aucune colonne de la matrice A ne peut s’écrire comme une combinaison linéaire des autres colonnes.
- Les lignes de la matrice A sont linéairement indépendantes : aucune ligne de la matrice A ne peut s’écrire comme une combinaison linéaire des autres lignes.
- Le noyau de la matrice A est l’ensemble nul (Niveau universitaire) : le seul élément du noyau de A est l’élément nul.

Comment savoir si un système admet une infinité de solutions ?
Considérons un système d’équations écrit sous la forme AX=B.
Le système admet une infinité de solutions si :
- La matrice A est rectangulaire et le rang de la matrice A est égal au rang de la matrice augmentée [A|B]
- La matrice A est rectangulaire et la matrice A est plein rang

Comment savoir si un système n’admet aucune solution ?
Considérons un système d’équations écrit sous la forme AX=B. Le système n’admet aucune solution s’il n’admet pas de solution unique et s’il n’admet pas une infinité de solution.
Le système n’admet pas de solution si:
- le rang de la matrice A est plus petit que le rang de la matrice augmentée [A|B]
- le système n’admet pas une unique solution et n’admet pas une infinité de solutions

Conseils et astuces
- Pour savoir si un système admet une solution, il faut d’abord l’échelonner
- Le rang d’une matrice est égal à son nombre de pivots
- Pour déterminer le rang d’une matrice, il faut d’abord l’échelonner
- Le déterminant d’une matrice rectangulaire n’existe pas.
- Si la matrice A est rectangulaire, alors le système admet une infinité de solutions ou une unique solution.
- Utilisez symbolab pour la résolution des systèmes d’équations linéaires.
Sujets similaires
- COMMENT SAVOIR SI UN SYSTÈME ADMET UNE SOLUTIONDécouvrez les trois types de solutions d’un système. Apprenez comment savoir si un système admet des solutions avec des exercices résolus.
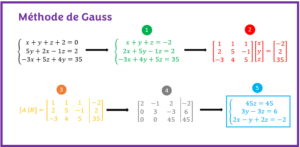
- MÉTHODE DE GAUSSL’objectif est d’apprendre à résoudre un système d’équations linéaires par la méthode de Gauss à partir d’exercices résolus.
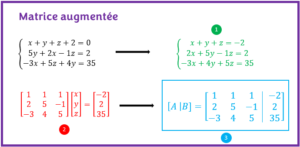
- MATRICE AUGMENTÉEL’objectif est d’apprendre à écrire la matrice augmentée d’un système d’équations et de l’échelonner à l’aide d’exercices résolus.
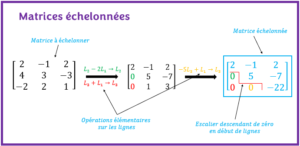
- MATRICES ÉCHELONNÉESL’objectif est d’apprendre à échelonner une matrice et à reconnaître les matrices échelonnées à l’aide d’exercices résolus.