L’objectif est d’apprendre la multiplication de matrice et de présenter les propriétés relatives au produit matriciel avec des exercices résolus.
Sommaire
La multiplication matricielle est l’une des opérations qui peuvent être effectuées sur les matrices en algèbre linéaire. Le produit matriciel est possible lorsque les deux matrices données, A et B sont compatibles. La multiplication matricielle est une opération binaire, qui donne une matrice à partir de deux matrices données.
Comme nous l’avons vu dans les articles précédents, les opérations d’addition et de soustraction peuvent aussi être réalisées sur les matrices. Explorons le concept de la multiplication matricielle en commençant par un rappel général très important sur les matrices.
Rappel et mise en contexte sur la multiplication de matrice
Une matrice est un tableau de ligne et de colonnes contenant des éléments. Il existe plusieurs matrices particulières parmi lesquelles on peut citer la matrice triangulaire, la matrice diagonale, la matrice identité et la matrice nulle. Vous trouverez la définition de chacune de ces matrices dans l’article sur les matrices et le langage matriciel.
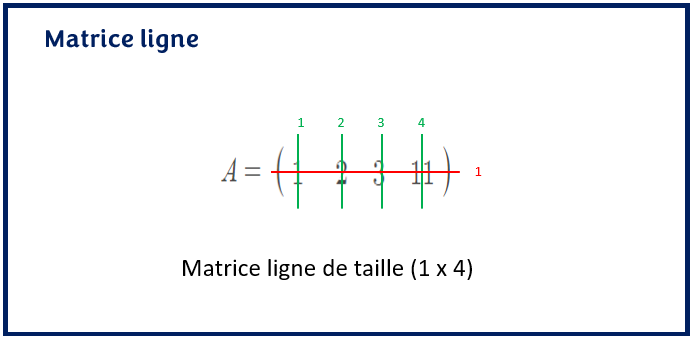
Une matrice ligne est une matrice qui a une ligne et plusieurs colonnes alors qu’une matrice colonne est une matrice qui a plusieurs lignes, mais une seule colonne.
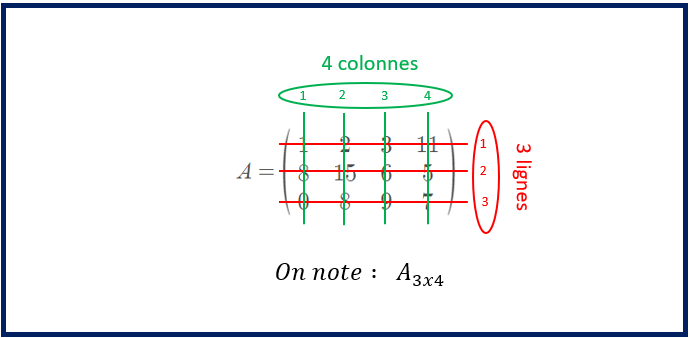
La dimension ou la taille d’une matrice est le nombre de lignes et le nombre de colonnes de la matrice. C’est un concept très important dans la multiplication de matrice. Nous verrons que pour multiplier deux matrices, il faudra d’abord étudier la compatibilité de la dimension de ces matrices.
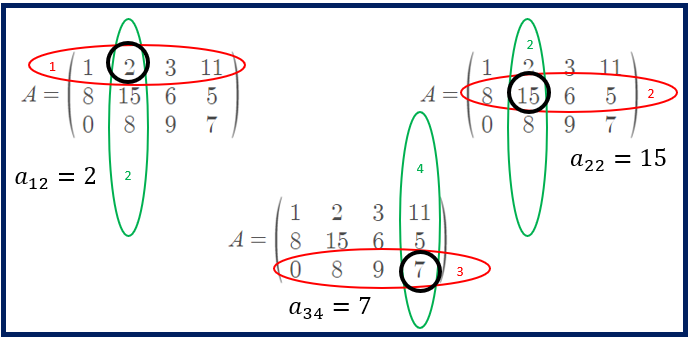
Les éléments d’une matrice notée aij sont identifiés en donnant la ligne et la colonne de l’élément. Par exemple, si le chiffre 7 est un élément d’une matrice A se trouvant à l’intersection de la troisième ligne et quatrième colonne alors on notera: a34 = 7. Il est très important de toujours commencer par lire le numéro de la ligne avant de lire le numéro de la colonne.
Maintenant que nous avons rappelé les concepts importants, nous avons tous les outils nécessaires pour comprendre la multiplication matricielle.
Condition de la multiplication de deux matrices
La multiplication de deux matrices est une matrice. En algèbre linéaire, la multiplication de matrice n’est possible que lorsque les matrices sont compatibles.
Compatibilité de la multiplication de matrice
Deux matrices A et B sont dites compatibles si et seulement si le nombre de colonnes de la matrice A est égal au nombre de lignes de la matrice B. Cela signifie que si A est une matrice d’ordre (m x n) et que B est une matrice d’ordre (n x p), alors on peut dire que les matrices A et B sont compatibles.
Il est donc nécessaire de connaître premièrement la dimension ou l’ordre des matrices à multiplier.
Illustration 1
L’illustration suivante résume le concept de compatibilité entre deux matrices
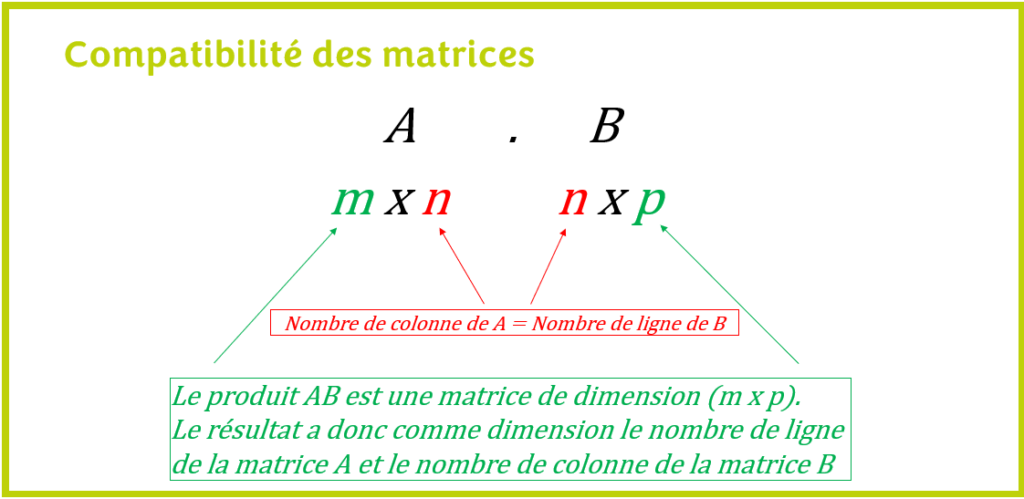
Ainsi, lorsqu’on multiplie deux matrices, la matrice que l’on obtient est une matrice de dimension ( m x p) où m est le nombre de lignes de la matrice A (matrice la plus à gauche) et p est le nombre de colonnes de la matrice B (matrice la plus à droite).
Considérons l’exemple suivant. Le produit de matrice est-il possible? si oui, quelle sera la dimension du résultat?

Dans le premier, le deuxième, le quatrième et le sixième cas, on remarque que le produit de matrice est possible, car les deux matrices sont compatibles c’est-à-dire que le nombre de colonnes de la matrice à gauche (code de couleur rouge) était égal au nombre de lignes de la matrice à droite(code de couleur rouge).
Aussi, on peut observer que dans chacun des cas respectifs, les résultats du produit des deux matrices E,F,H et J avaient systématiquement pour dimension le nombre de lignes de la matrice de gauche (code de couleur bleu) et le nombre de colonnes de la matrice de droite(code de couleur vert).
Dans le troisième et cinquième cas, la multiplication de matrice est impossible, car les deux matrices ne sont pas compatibles c’est-à-dire que le nombre de colonnes de la matrice à gauche n’est pas égal au nombre de ligne de la matrice à droite (voir les cercles noirs).
Multiplication de matrice carrée
Multiplication de matrice 2 X 2
La multiplication de matrice 2×2 ou le produit de matrice a des règles à respecter et une méthodologie tout comme l’addition et la soustraction matricielle. Afin de multiplier deux matrices, nous multiplions les éléments de chaque ligne de la première matrice par les éléments de chaque colonne de la deuxième matrice (élément par élément) comme indiqué dans l’illustration 2. Enfin, nous additionnons les résultats de chacun de ces produits. Le résultat du produit de deux matrices carrées 2×2 est à nouveau une matrice carrée 2×2.
Illustration 2
L’illustration suivante résume le concept de la multiplication de matrice carrée 2×2
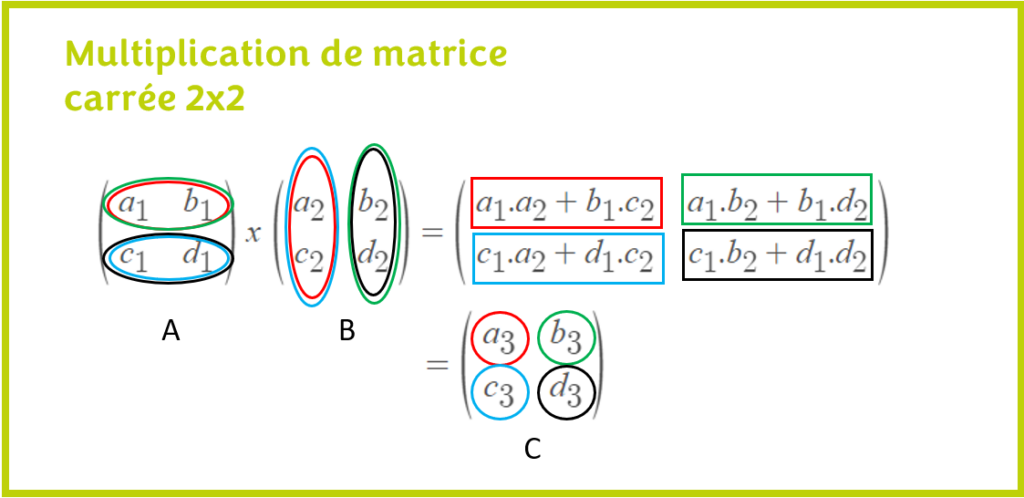
Le produit d’une matrice par une autre matrice est une matrice. Ici, on voit que les matrices A et B sont compatibles, donc le produit de A par B est possible. On a alors A x B = C.
Puisque le résultat du produit de A par B est la matrice C de dimension (2×2), alors, il faut donc calculer quatre coefficients pour compléter l’opération de la multiplication matricielle.
Les coefficients à déterminer pour la matrice C sont donc :
- a3 correspondant au coefficient c11 (élément de la première ligne première colonne de la matrice C) – code de couleur rouge
- b3 correspondant au coefficient c12 (élément de la première ligne deuxième colonne de la matrice C) – code de couleur verte
- c3 correspondant au coefficient c21 (élément de la deuxième ligne première colonne de la matrice C) – code de couleur bleue
- d3 correspondant au coefficient c21 (élément de la deuxième ligne deuxième colonne de la matrice C) – code de couleur noir
Il est important de remarquer que chaque coefficient à déterminer donne la recette pour le calculer.
Voyons maintenant le tout dans un exemple pratique.
Considérons l’exemple suivant :

On remarque que la matrice C, le résultat de la multiplication de la matrice A par la matrice B, est de dimension (2 x 2) donc il y’a quatre coefficients à déterminer. Chacun de ces coefficients donne la recette pour le calculer:
- Le coefficient C11= 32 s’obtient en multipliant élément par élément la première ligne de la matrice A par la première colonne de la matrice B
- Le coefficient C12= 13 s’obtient en multipliant élément par élément la première ligne de la matrice A par la deuxième colonne de la matrice B
- Le coefficient C21= 57 s’obtient en multipliant élément par élément la deuxième ligne de la matrice A par la première colonne de la matrice B
- Le coefficient C22= 24 s’obtient en multipliant élément par élément la deuxième ligne de la matrice A par la deuxième colonne de la matrice B
Vous trouverez des explications plus détaillées sur comment multiplier des matrices.
Multiplication de matrice 3X3
La multiplication de matrice 3×3 ou le produit de matrice 3×3 respecte les mêmes règles et les mêmes conditions que la multiplication matricielle de matrice 2×2. Les deux matrices doivent donc être compatibles.
La multiplication matricielle se fait toujours d’élément à élément en multipliant tour à tour chaque ligne de la première matrice par chaque colonne de la deuxième matrice. En suivant cette méthode, le produit de matrice 3×3 nous permet de déterminer les 9 coefficients de la matrice résultat.
Illustration 3
L’illustration suivante résume le concept de la multiplication de matrice carrée 3×3
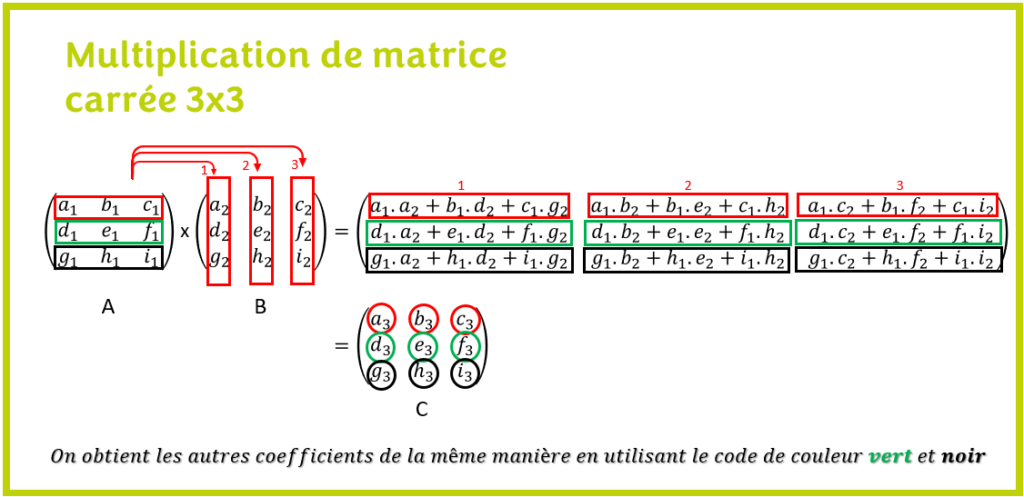
Le produit d’une matrice par une autre matrice est une matrice. Ici, on voit que les matrices A et B sont compatibles, donc le produit de A par B est possible. On a alors A x B = C.
Puisque le résultat du produit de A par B est la matrice C de dimension (3×3), alors, il faut donc calculer neuf coefficients pour compléter l’opération de la multiplication matricielle.
La multiplication matricielle de deux matrices se fait de façon méthodique et ordonnée.
Comme pour la multiplication de matrice carrée 2×2, il est important de remarquer que chaque coefficient à déterminer donne la recette pour le calculer.
Considérons l’exemple suivant :
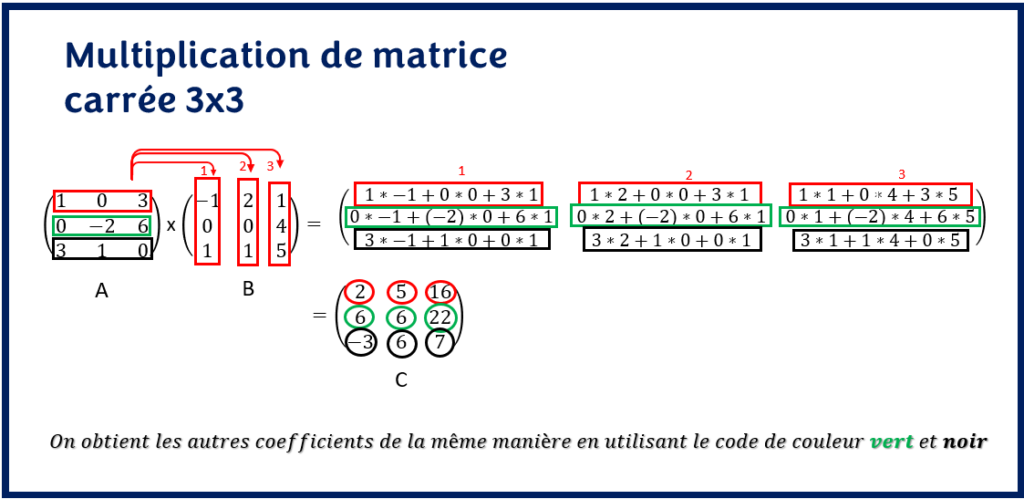
On remarque que la matrice C, le résultat de la multiplication de la matrice A par la matrice B, est de dimension (3 x 3) donc il y’a neuf coefficients à déterminer. Chacun de ces coefficients donne la recette pour le calculer:
- Le coefficient C11= 2 s’obtient en multipliant élément par élément la première ligne de la matrice A par la première colonne de la matrice B
- Le coefficient C12= 5 s’obtient en multipliant élément par élément la première ligne de la matrice A par la deuxième colonne de la matrice B
- etc
On recommence la procédure en utilisant cette fois la deuxième ligne de la matrice A (code de couleur vert)
- Le coefficient C21= 6 s’obtient en multipliant élément par élément la deuxième ligne de la matrice A par la première colonne de la matrice B
- Les coefficients C22= 6 et C23= 22 se déduisent de cette même manière
Vous trouverez des explications plus détaillées sur comment multiplier des matrices.
Multiplication de matrice rectangulaire
La multiplication de matrice rectangulaire est exactement la même que la multiplication de matrice carrée. Il faut alors vérifier si le produit de matrice est possible en étudiant la compatibilité des deux matrices.
Multiplication de matrices de taille différentes
La première étape avant d’effectuer le produit matriciel est de vérifier la compatibilité des matrices par la connaissance de chacune des dimensions des deux matrices.
Illustration 4
L’illustration suivante résume effectivement le concept de la multiplication de matrices de taille différentes
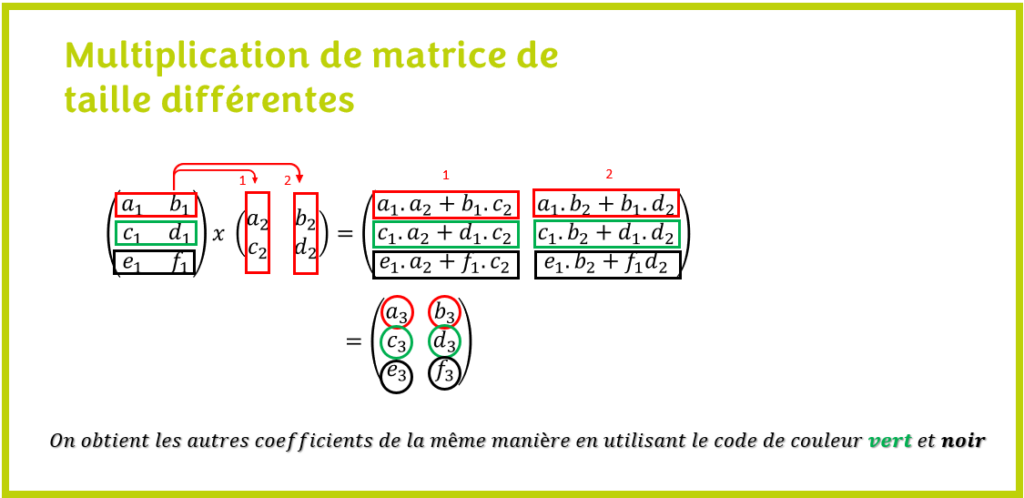
Le produit d’une matrice par une autre matrice est une matrice. Ici, on voit que les matrices A et B sont compatibles, donc le produit de A par B est possible. La matrice A est de dimension (3 x 2) et la matrice B est de dimension (2 x 2). La matrice C devra alors être de dimension (3 x 2) : A x B = C.
Puisque le résultat du produit de A par B est la matrice C de dimension (3 x 2), alors, il faut donc calculer six coefficients pour compléter l’opération de la multiplication matricielle.
Calcul des coefficients
Comme pour la multiplication de matrice carrée, il est important de remarquer que chaque coefficient à déterminer donne la recette pour le calculer. Ainsi, les six coefficients s’obtiennent comme suite:
- D’abord, concernant le code de couleur rouge ci bas, prendre la première ligne de la matrice à gauche (matrice A) et la multiplier tour à tour, élément à élément, avec chaque colonne de la deuxième matrice à droite (matrice B). On obtient ainsi les deux premiers coefficients de la première ligne de la matrice C. Ces coefficients sont: c11 et c12.
Considérons l’exemple suivant:
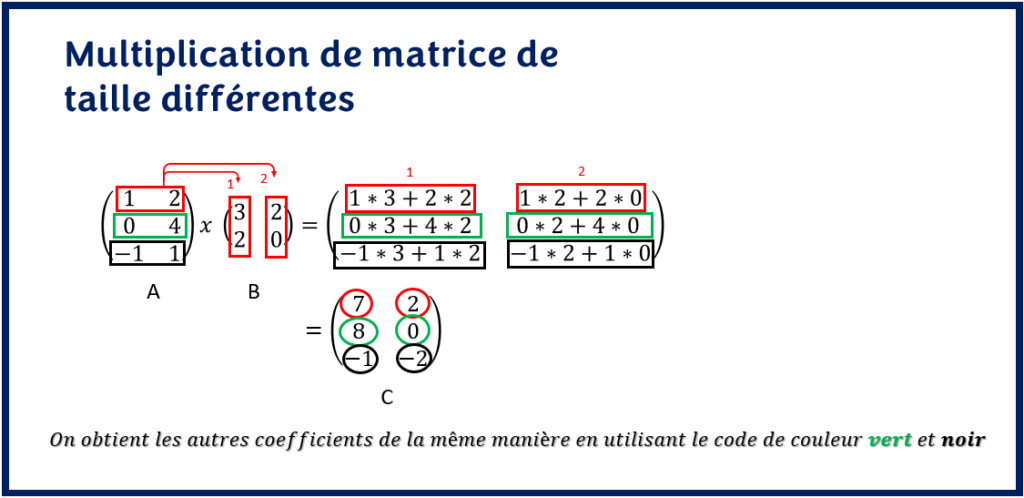
En outre, on remarque que le produit de matrice de taille différente est toujours une matrice. Ici, la matrice A est de taille (3 x 2) et la matrice B est de taille (2 x 2). Puisqu’il y’a compatibilité entre les deux matrices, la matrice C est une matrice de dimension (3 x 2). On aura donc six coefficients à calculer :
Première ligne de la matrice C (code de couleur rouge)
- Le coefficient C11= 7 s’obtient en multipliant élément par élément la première ligne de la matrice A par la première colonne de la matrice B
- Le coefficient C12= 2 s’obtient en multipliant élément par élément la première ligne de la matrice A par la deuxième colonne de la matrice B
Deuxième ligne de la matrice C (code de couleur vert)
- Le coefficient C21= 8 s’obtient en multipliant élément par élément la deuxième ligne de la matrice A par la première colonne de la matrice B
- Le coefficient C22= 0 s’obtient en multipliant élément par élément la deuxième ligne de la matrice A par la deuxième colonne de la matrice B
Vous trouverez des explications plus détaillées sur comment multiplier des matrices.
Multiplication d’une matrice par un scalaire
Produit d’une matrice par un scalaire
En fait, la multiplication d’une matrice par un scalaire est la plus simple des multiplications. En effet, cela revient à multiplier tous les chiffres de la matrice par ce scalaire.
Pour rappel, un scalaire est un chiffre réel défini dans IR. Tous les nombres sont des scalaires.
Le produit d’une matrice par un scalaire est toujours possible, peu importe sa taille ou sa dimension. Regardons cela ensemble.
Illustration 5
Considérons l’illustration suivante :

La multiplication d’une matrice par un scalaire est une matrice de la même dimension que la matrice initiale. Le produit de la matrice par le scalaire se fait élément à élément.
Considérons l’exemple suivant :

La dimension de la matrice à multiplier par le scalaire n’a pas d’importance. On multiplie tout simplement chaque coefficient de la matrice par le scalaire. On obtient ainsi une matrice de même dimension.
La méthode est la même pour des matrices carrées ou rectangulaires.
Propriété de la multiplication de matrice
Tout comme l’addition et la soustraction de matrice, la multiplication de matrices a des propriétés définies par l’algèbre linéaire.
Non-commutativité
Le produit de matrice est non commutatif. Le produit de A par B est généralement différent du produit de B par A : A.B ≠ B.A
La raison principale de cette propriété est la compatibilité des matrices.
Exemple 6
Considérons l’exemple suivant:

Le produit de matrice de A par B est généralement différent du produit de B par A. Cet exemple l’illustre bien.
Si le produit de deux matrices est commutatif, alors l’une des matrices est l’inverse de l’autre.
Associativité
La multiplication de matrice est associative c’est-à-dire (AB)C = A(BC).
En d’autres termes, on pourrait effectuer le produit de deux matrices dans l’ordre de notre choix. Les parenthèses peuvent être déplacées afin de gérer les priorités.
Distributivité
La multiplication matricielle obéit à la propriété de distributivité c’est-à-dire A(B+C) = AB + AC.
Cependant, il est très important de respecter l’ordre dans lequel on multiplie les matrices. Par exemple, on ne pourrait pas faire développement suivant : A(B+C)= BA +CA. En effet, cette opération n’est pas possible, car le produit de matrice n’est pas commutatif.
Notons que la distributivité n’est possible que si les matrices A,B et C sont compatibles.
Produit avec un scalaire
Le produit de matrice par un scalaire est défini par l’opération suivante : C(AB) = (CA)B = A(BC)
où c est un scalaire.
La multiplication par un scalaire peut se faire dans l’ordre de notre choix. Toutefois, il ne faut pas changer les positions des matrices A et B.
Transposée d’un produit de matrice
La transposition d’un produit de matrice est aussi définie pour la multiplication. Par conséquent, elle respecte la propriété suivante : (AB)T= BTAT
où T désigne la transposée.
Déterminant d’un produit de matrice
Le déterminant d’un produit de matrice est le produit des déterminants. Si A et B sont deux matrices, alors la propriété suivante est valide : det (AB) = det(A) . det(B).
Conseils et astuces sur la multiplication de matrice
- La multiplication matricielle consiste en des opérations successives de multiplication de lignes par des colonnes.
- La multiplication de matrice est définie seulement lorsque les matrices sont compatibles
- La dimension du produit matriciel est définie par le nombre de lignes de la première matrice et le nombre de colonnes de la seconde
- Le produit matriciel A.B est généralement différent du produit B.A
- Pour multiplier plusieurs matrices, on effectue des produits de deux matrices successivement jusqu’à l’obtention du résultat (une matrice)
- La multiplication de matrice obéit à la propriété de distributivité sur l’addition ou la soustraction de matrice
En résumé
Temps nécessaire : 1 minute
COMMENT MULTIPLIER DES MATRICES?
- Déterminer la dimension des deux matrices
La dimension d’une matrice est le nombre de lignes et de colonnes de la matrice. Par exemple, la matrice A est de dimension (3 x 4).

- Vérifier que les deux matrices sont compatibles
Deux matrices sont compatibles si le nombre de colonnes de la première matrice à gauche est égal au nombre de ligne de la deuxième matrice à droite

- Effectuer le produit des matrices
La multiplication de matrice s’effectue en multipliant chaque ligne la matrice à gauche par chaque colonne de la matrice à droite. Outre cela, la connaissance du numéro de la ligne i et du numéro de la colonne j permet de trouver le coefficient aij de la matrice du résultat.

Exercices
Ceci est une série d’exercices résumant l’ensemble des enseignements étudiés dans ce cours. Vous trouverez la solution pour chacun de ces problèmes dans la section du solutionnaire.
Vous pouvez aussi utiliser cet outil pour effectuer vos calculs.
Solutions
FAQ sur la multiplication de matrice
De toute évidence, la multiplication matricielle est importante pour faciliter les calculs en algèbre linéaire. Les matrices permettent d’effectuer des millions d’opérations à des temps très courts en utilisant les ordinateurs. C’est d’ailleurs tout l’intérêt de la multiplication matricielle. C’est un outil important dans de nombreux domaines des mathématiques, de la physique, et l’ingénierie.
La multiplication de matrice est possible si les matrices sont compatibles c’est-à-dire si le nombre de colonnes de la première matrice(celle à gauche) est égal au nombre de ligne de la deuxième matrice (celle de droite).
En général, la multiplication de matrice n’est pas commutative. Il existe des cas où elle est commutative. Par exemple, la multiplication d’une matrice par son inverse.
Non, le produit n’est pas possible, car les deux matrices ne sont pas compatibles. En effet, le nombre de colonnes de la première matrice (2) n’est pas égal au nombre de ligne de la deuxième matrice (3).
La multiplication de matrice s’effectue en multipliant chaque ligne la matrice à gauche par chaque colonne de la matrice à droite. La connaissance du numéro de la ligne i et du numéro de la colonne j permet de trouver le coefficient aij de la matrice du résultat.
Oui, on peut multiplier une matrice par un chiffre. Cela s’appelle la multiplication par un scalaire. Il suffit tout simplement de multiplier tous les éléments de la matrice par ce chiffre.
Pour transposer deux matrices, il suffit de transposer chacune des matrices et changer leurs ordres d’apparition. La transposée respecte la propriété suivante : (AB)T= BTAT
Sujets similaires
- OPÉRATIONS SUR LES MATRICESL’objectif est de présenter les opérations de bases sur les matrices : addition, soustraction, multiplication, transposé, déterminant et inverse à partir d’exercices résolus.
- COMMENT MULTIPLIER DES MATRICES?Vous trouverez les étapes nécessaires et suffisantes sur comment multiplier des matrices avec des exemples pratiques.
- COMMENT TRANSPOSER UNE MATRICE?Vous trouverez les étapes nécessaires et suffisantes sur comment transposer une matrice avec des exemples pratiques.
- TRANSPOSÉE D’UNE MATRICEL’objectif est d’apprendre à faire la transposée d’une matrice et découvrir les propriétés relatives à la transposition de matrice avec des exercices résolus.