L’objectif ici est d’apprendre à utiliser les rapports trigonométriques pour calculer une mesure manquante ou un angle manquant dans un triangle rectangle avec des exemples résolus.
Sommaire
Rappel et mise en contexte
Le triangle rectangle est l’une des figures géométriques(carré, rectangle, cercle, trapèze, polygone) les plus utilisées en géométrie. Plusieurs formules et relations mathématiques permettent de calculer les mesures manquantes pour ce type de figure en particulier. Parmi ces relations à utiliser dans le triangle rectangle, nous avons: la relation de Pythagore, les relations métriques et les rapports trigonométriques.
Dans ce cours, nous allons nous intéresser aux rapports trigonométriques. Un rapport trigonométrique est une relation unique entre deux côtés d’un triangle rectangle. Connaissant un angle aigu, six rapports trigonométriques peuvent être définis dans un triangle rectangle à savoir: le sinus, cosinus, la tangente, la sécante, la cosécante et la cotangente.
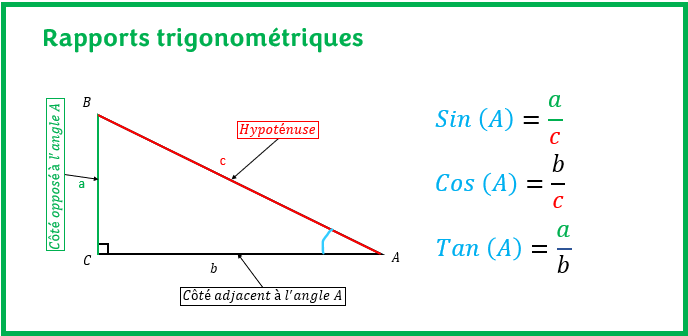
On s’intéressera dans un premier temps aux trois premières relations trigonométriques. Avant toute chose, il est important de définir le vocabulaire associé à ce concept.
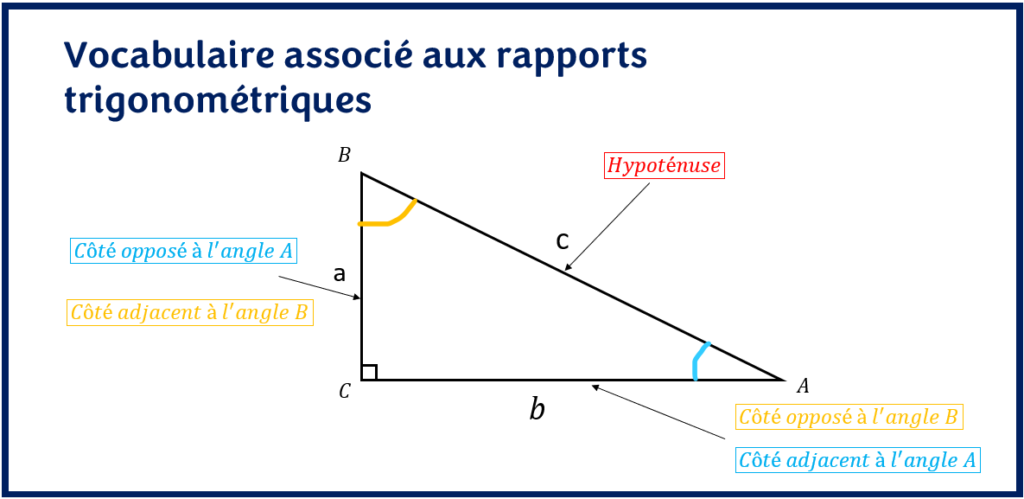
Une cathète du triangle peut être à la fois côté opposé ou côté adjacent. Tout dépend de l’angle considéré pour le calcul.
Rapports trigonométriques : Sinus, Cosinus et Tangente
Les relations trigonométriques du sinus, cosinus et la tangente d’un angle sont récapitulées ci-dessous:

Plus simplement, le côté adjacent à un angle est le côté autre que l’hypoténuse qui sert à former cet angle. Le côté opposé à un angle quant à lui est le troisième côté qui ne sert pas à former cet angle.
Une façon simple de retenir les trois formules des rapports trigonométriques est l’abréviation:
SOH – CAH – TOA
S pour sinus, C pour cosinus, T pour tangente, O pour côté opposé à l’angle, A pour côté adjacent à l’angle et H pour hypoténuse.
Ainsi, on lit donc:
Sinus est égale au côté opposé sur l’hypoténuse, Cosinus est égale au côté adjacent sur hypoténuse et la Tangente est égale au côté opposé sur le côté adjacent.
Équivalence des rapports trigonométriques
En général, il existe une relation d’équivalence entre ces rapports. Si l’on observe les relations précédentes, on peut déduire que:
- Le sinus d’un angle est égal au cosinus de l’angle qui est complémentaire à cet angle
- Le cosinus d’un angle est égal au sinus de l’angle qui est complémentaire à cet angle
- la tangente d’un angle est égale à l’inverse de la tangente de l’angle qui est complémentaire à cet angle
- la tangente d’un angle est aussi égale au rapport entre le sinus et le cosinus de cet angle
Vérifions ces constats à travers cet exemple:

Lorsque la valeur décimale d’un rapport trigonométrique est demandée, le résultat doit être arrondi au dix millième près c’est-à-dire quatre chiffres après la virgule.
Calcul d’une mesure manquante avec les rapports trigonométriques
Dans un triangle rectangle, les rapports trigonométriques permettent de calculer la mesure d’un côté manquant. Pour cela, il est important de connaître la mesure d’un angle aigu et la mesure d’un côté.
Pour déterminer la mesure manquante d’un côté dans un triangle rectangle, il faut suivre les étapes suivantes:
- Écrire la mnémotechnique : SOH – CAH – TOA
- Faire l’inventaire des mesures connues:
- Si la mesure d’un angle est connue dans le triangle, alors l’on peut calculer le sinus, le cosinus ou la tangente de cet angle. Cocher le S, C et T dans SOH – CAH – TOA
- Si la mesure d’un côté du triangle est connue, identifier s’il s’agit du côté opposé à l’angle, du côté adjacent ou de l’hypoténuse. Cocher le O, A ou H dans SOH – CAH -TOA
- Identifier et nommer la mesure manquante à calculer:
- La mesure du côté à calculer est-elle le côté opposé ou le côté adjacent à l’angle ou l’hypoténuse? Cocher le O, A ou H dans SOH – CAH – TOA
- Identifier le rapport trigonométrique à utiliser à partir des informations cochées.
Considérons les exemples suivants:

En se référant à la méthodologie précédente, on obtient la bonne formule à utiliser d’une façon mécanique et évidente. Les informations cochées en noir sont des données connues et en rouge la donnée inconnue c’est-à-dire la mesure manquante. Une fois la bonne formule sélectionnée, il ne reste plus qu’à isoler la mesure manquante.
Calcul d’un angle manquant avec les rapports trigonométriques
Pour calculer la mesure d’un angle manquant dans un triangle rectangle, il faut connaître au moins deux mesures des côtés du triangle.
La méthodologie de résolution est la même qu’à la section précédente.
Considérons les exemples suivants:
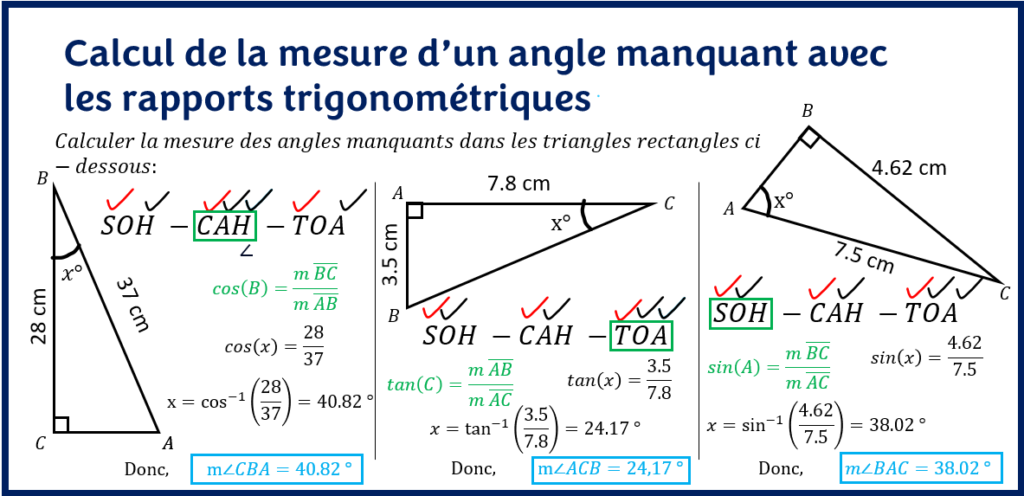
Ici, puisque c’est l’angle qui est l’inconnu (la mesure manquante), alors on coche en rouge les sinus, cosinus et la tangente. Ensuite, les données du problème sont cochées en noir. Enfin, on choisit le rapport trigonométrique approprié pour calculer l’angle.
Lorsque l’on cherche l’angle manquant, on calcule soit le sin-1(x), le cos-1(x) ou la tan-1(x).
Conseils et astuces
- Un angle aigu est un angle donc la mesure est plus petite que 90 degrés.
- Utiliser la mnémotechnique SOH-CAH-TOA pour se souvenir des formules des rapports trigonométriques.
- Se souvenir des équivalences trigonométriques en particulier: tan(A) = sin(A)/cos(A)
- Pour calculer la mesure manquante d’un côté dans un triangle rectangle avec les rapports trigonométriques, il faut connaître au moins un angle et une mesure d’un côté.
- Pour calculer la mesure d’un angle manquant dans un triangle rectangle avec les rapports trigonométriques, il faut connaître au moins la mesure de deux côtés du triangle.
- Les fonctions réciproques sin-1(x), cos-1(x) et tan-1(x) permettent de calculer la mesure de l’angle correspondant.
- Lorsque le triangle n’est pas rectangle, on utilise plutôt la loi des sinus ou la loi des cosinus
- Vous pouvez consulter cette vidéo sur les rapports trigonométriques pour le calcul d’une longueur manquante.
- Si à la fin de la lecture de ce cours, vous ne comprenez toujours pas, vous pouvez demander l’assistance d’un tuteur en ligne par courriel.
FAQ
Les rapports trigonométriques dans un triangle rectangle sont le cosinus, le sinus, la tangente, la sécante, la cosécante et la cotangente. Ces rapports permettent de déterminer des mesures manquantes ou des angles manquants dans un triangle rectangle.
Un rapport trigonométrique est une relation unique entre la mesure de deux côtés d’un triangle rectangle. Il en existe six dans un triangle rectangle (le cosinus, le sinus, la tangente, la sécante, la cosécante et la cotangente). Pensez à la mnémotechnique : SOH – CAH – TOA ou CAH – SOH – TOA.
Pour calculer les rapports trigonométriques, il faut d’abord se rappeler des formules trigonométriques. Pensez à la mnémotechnique SOH – CAH – TOA. Ensuite, à travers le problème, faites l’inventaire des données connues et l’inventaire des données inconnues ou recherchées. Enfin, utiliser le rapport trigonométrique appropriée. Vous pouvez regarder comment calculer une mesure manquante ou un angle manquant dans un triangle rectangle avec les rapports trigonométriques.
Il existe six formules trigonométriques dans un triangle rectangle. Ces formules sont:
– sin(A) = (côté opposé à l’angle)/(Hypoténuse)
– cos(A) = (côté adjacent à l’angle)/(Hypoténuse)
– tan(A) = (côté opposé à l’angle)/(côté adjacent à l’angle)
– sec(A) = 1/cos(A)
– cosec(A) = 1/sin(A)
– cotan(A) = 1/tan(A)
La trigonométrie est l’ensemble des relations mathématiques utilisant les angles. Dans un triangle rectangle par exemple, les rapports trigonométriques nous permettent de calculer les mesures des côtés manquants ou des angles manquants. Regardez les exemples ci-dessus pour comprendre comment les utiliser.
Sujets similaires
- Périmètre d’un losangeL’objectif est d’apprendre à calculer le périmètre d’un losange et de connaitre ses propriétés avec des exemples résolus.
- Aire d’un cercleL’objectif est d’apprendre comment calculer l’aire d’un cercle et de connaitre ses propriétés avec des exemples résolus.
- Aire d’un triangle rectangleL’objectif est d’apprendre comment calculer l’aire d’un triangle rectangle de plusieurs façons différentes avec des exercices résolus.
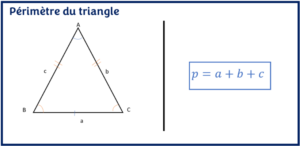
- Périmètre du triangleL’objectif est d’apprendre à calculer le périmètre du triangle et de connaître ses propriétés à partir d’exercices résolus.
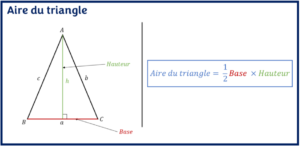
- Aire du triangleL’objectif est d’apprendre à calculer l’aire d’un triangle et de connaître ses propriétés à partir d’exercices résolus.
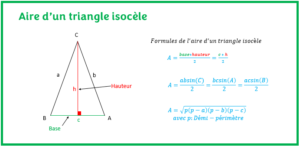
- Aire d’un triangle isocèleL’objectif est d’apprendre à calculer l’aire d’un triangle isocèle de plusieurs façons différentes avec des exercices résolus.
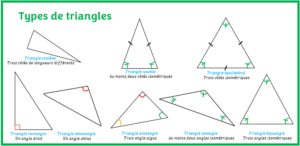
- Les types de trianglesL’objectif est d’apprendre les différents types de triangles existants et leurs propriétés avec des exemples résolus.
- Périmètre du rectangleL’objectif est d’apprendre à calculer le périmètre du rectangle et de connaître ses propriétés à partir d’exercices résolus.