Aire d’un cercle

L’objectif est d’apprendre comment calculer l’aire d’un cercle et de connaitre ses propriétés avec des exemples résolus.

Sommaire

Rappel et mise en contexte relatif à l’aire du cercle

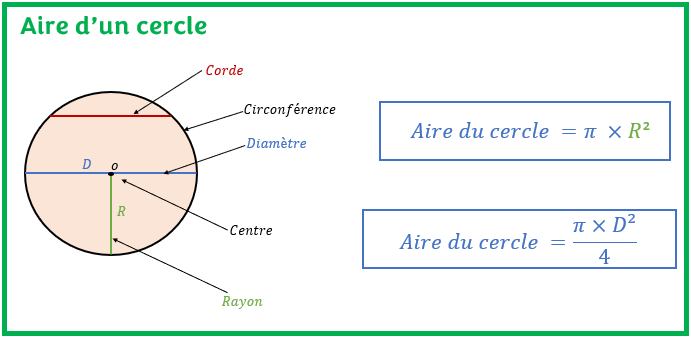
Dans un article précédent, nous avons vu comment calculer l’aire et le périmètre d’autres figures géométriques comme le triangle, le rectangle, le carré, le losange et le trapèze. C’est dans cet ordre idée que nous allons voir aujourd’hui comment calculer l’aire du cercle. Le cercle est une figure géométrique formée par un ensemble de points situés à une distance donnée (rayon) d’un point fixe (centre) sur le plan. Le point fixe est appelé l’origine du cercle ou centre du cercle. La distance fixe entre le centre du cercle et ces points est appelée le rayon. La mesure du pourtour du cercle est appelée la circonférence ou le périmètre du cercle. Observez la figure suivante pour voir les parties de base d’un cercle, le centre, le rayon et le diamètre d’un cercle.

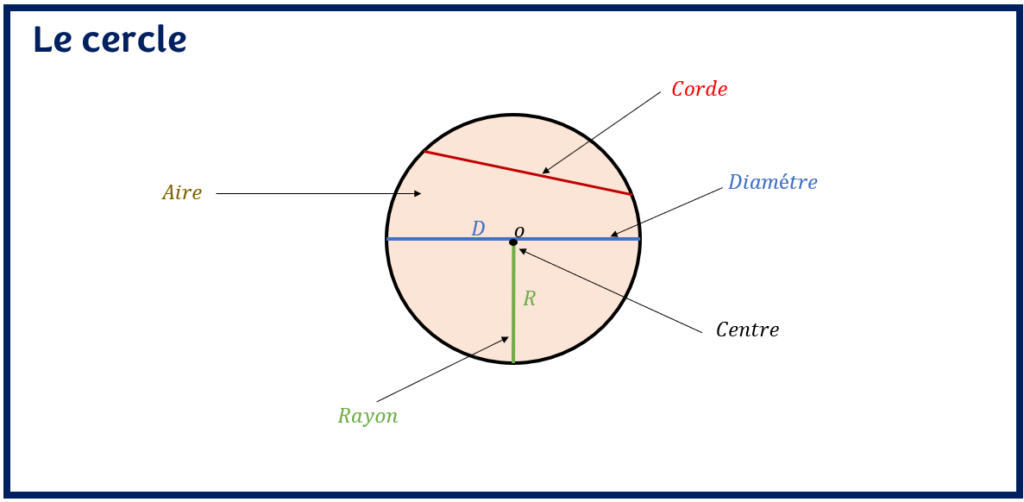
Une droite ou segment de droite qui relie deux points quelconques du cercle est appelé corde. Si en plus, la ligne relie deux points quelconques du cercle passe par le centre du cercle alors, la corde est appelée diamètre. En d’autres termes, toutes les cordes passant par le centre d’un cercle sont des diamètres. Elles ont donc la même longueur. Le diamètre est la plus longue corde d’un cercle. On peut donc conclure que chaque diamètre est une corde, mais que chaque corde n’est pas forcément un diamètre.

De nombreux objets qui nous entourent dans le monde réel sont de forme circulaire(cercle). On peut citer : l’anneau, le disque, le bracelet, une pièce de monnaie, une roue et un bouton pour ne citer que ceux-là.

Quelques bases avant le calcul de l’aire d’un cercle

Le rayon du cercle

Le rayon d’un cercle est une droite qui relie le centre du cercle à un point situé sur le contour du cercle. La mesure du rayon du cercle reste la même du centre jusqu’à n’importe quel point situé sur son périmètre.

Le rayon d’un cercle est la moitié de la mesure du diamètre du cercle. La formule de rayon du cercle est :

r = D/2

Où, r = rayon du cercle et D : Diamètre du cercle

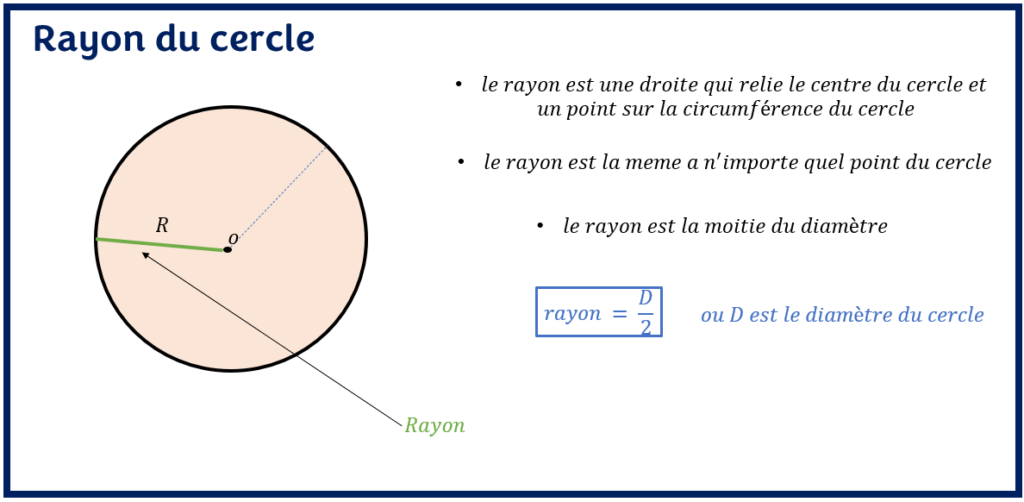
Pour un cercle donné, une corde ne peut jamais être un rayon du cercle, car le rayon ne répond pas à la définition d’une corde du cercle. En effet, le rayon ne relie jamais deux points du cercle situés sur ses contours.

Le diamètre du cercle

Un diamètre est un segment de droite qui passe par le centre et dont les extrémités se trouvent sur la circonférence d’un cercle. Pour rappel, la circonférence d’un cercle est encore appelée le périmètre du cercle. C’est une mesure de la longueur des contours du cercle.

Le diamètre est la plus longue corde d’un cercle. Un diamètre est la somme de deux rayons. On peut l’observer sur la figure ci-dessous :

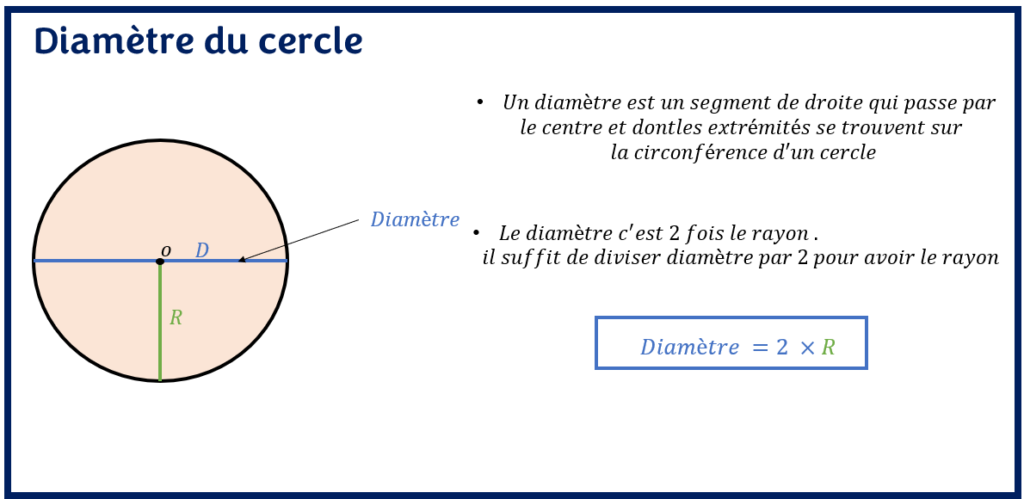
Lorsque le rayon du cercle n’est pas connu, on peut obtenir le diamètre du cercle de façon différente si l’on connait la circonférence du cercle ou son aire.

Par exemple, puisque l’on sait que la circonférence du cercle est le produit de la constante pi et du diamètre du cercle, on peut donc déduire le diamètre du cercle en appliquant la formule ci-dessous :

D = C\π

où, C : Circonférence ou périmètre du cercle

le diamètre = 2*R ou R est le rayon
Lorsque l′ aire est connues, le diamètre est égale a D =2*√(A/π)

La constante Pi (π)

La constante Pi noté π est une constante mathématique qui est le rapport entre la circonférence d’un cercle et son diamètre, approximativement égal à 3,14159265358979. C’est un nombre irrationnel qui apparaît dans de nombreuses formules en mathématiques et en physique. Un nombre irrationnel est un nombre réel qui ne peut pas être exprimé comme le quotient de deux entiers, c’est-à-dire qu’il ne peut pas être écrit sous forme de fraction.

Dans la plupart des exercices, la constante Pi (π) est approximée par 3,14.

La circonférence du cercle

En mathématique, la circonférence de toute figure définit la longueur du chemin ou de la limite qui l’entoure. En réalité, le terme circonférence est réservé uniquement au cercle. Pour les autres figures géométriques, on parle de périmètre. La circonférence et le périmètre sont donc deux expressions équivalentes quand il s’agit d’un cercle. Comme pour les autres figures géométriques, le périmètre et l’aire du cercle sont les deux grandeurs qui vont nous intéresser.

La circonférence du cercle est une mesure de la longueur des contours du cercle. Son unité est donc le mètre (m). On peut également l’exprimer à l’aide des autres multiples du mètre notamment le centimètre (cm). La formule de la circonférence du cercle connaissant le rayon est donc :

C = 2 * π * r

Où, C: circonférence ou périmètre du cercle, r : rayon du cercle

Si le diamètre du cercle est connu, la formule de la circonférence du cercle devient :

C = π * D

Où, C: circonférence ou périmètre du cercle, D: diamètre du cercle

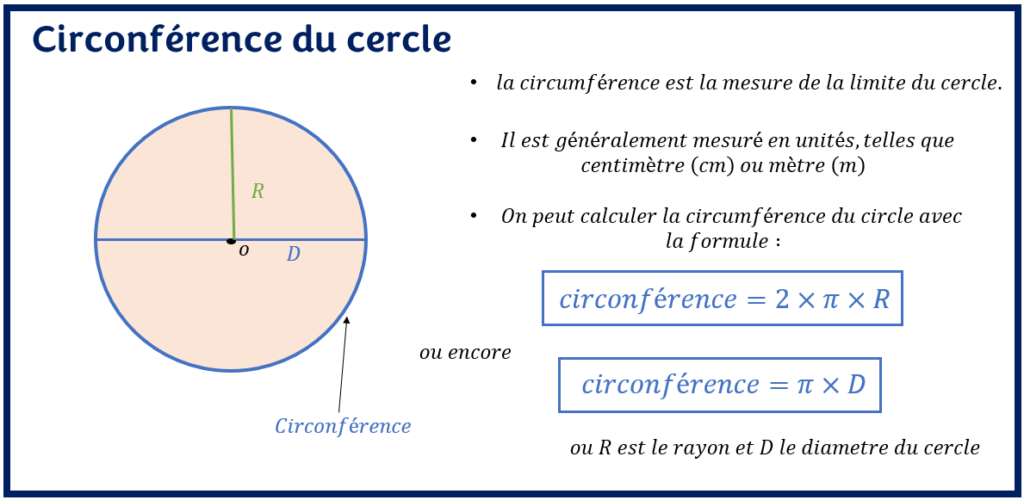
Lorsque nous utilisons la formule pour calculer la circonférence du cercle, le rayon du cercle est pris en compte. Il faut donc connaitre la valeur du rayon ou du diamètre pour évaluer le périmètre du cercle. On rappelle que le diamètre est le double du rayon.

Formule de l’aire du cercle

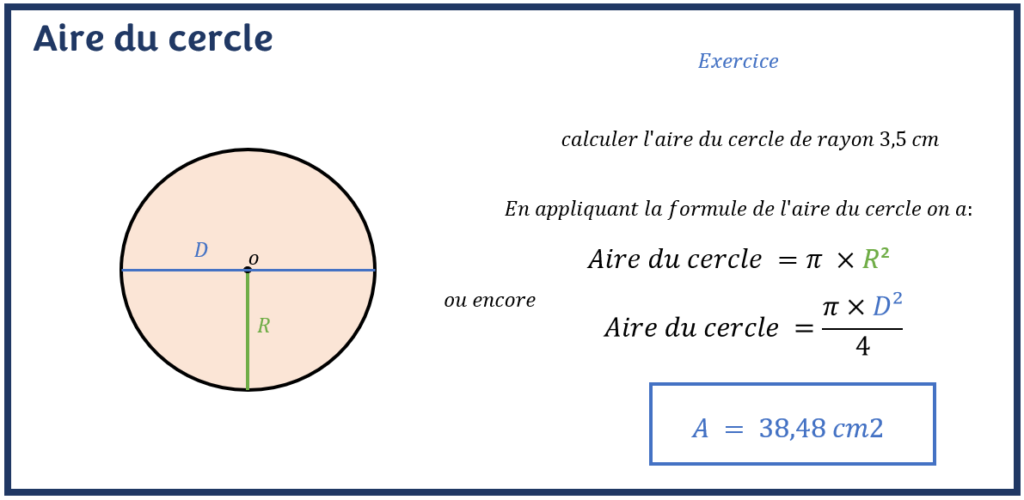
L’aire du cercle est une mesure de la région occupée par l’intérieur du cercle dans le plan. Si l’on connait la mesure du rayon du cercle, le calcul de l’aire ou de la surface du cercle devient trivial. La formule de l’aire du cercle est donc :

A = π* r²

Où, A : Aire ou surface du cercle , r : rayon du cercle

L’unité de la surface du cercle est le mètre carré (m2). Il peut aussi être exprimé à partir des multiples du mètre carré notamment le centimètre carré(cm²).

Lorsque le rayon du cercle n’est pas connu et que le diamètre du cercle est connu, l’on peut tout simplement calculer la mesure du rayon du cercle premièrement avant de calculer son aire une fois le résultat obtenu. Le rayon représente la moitié du diamètre du cercle.

On pourrait directement calculer l’aire ou la surface du cercle connaissant son diamètre en utilisant la formule suivante :

A = ( π * D²) / 4

Où, A : Aire ou surface du cercle, D: Diamètre du cercle

Calcul de l’aire d’un cercle connaissant son périmètre

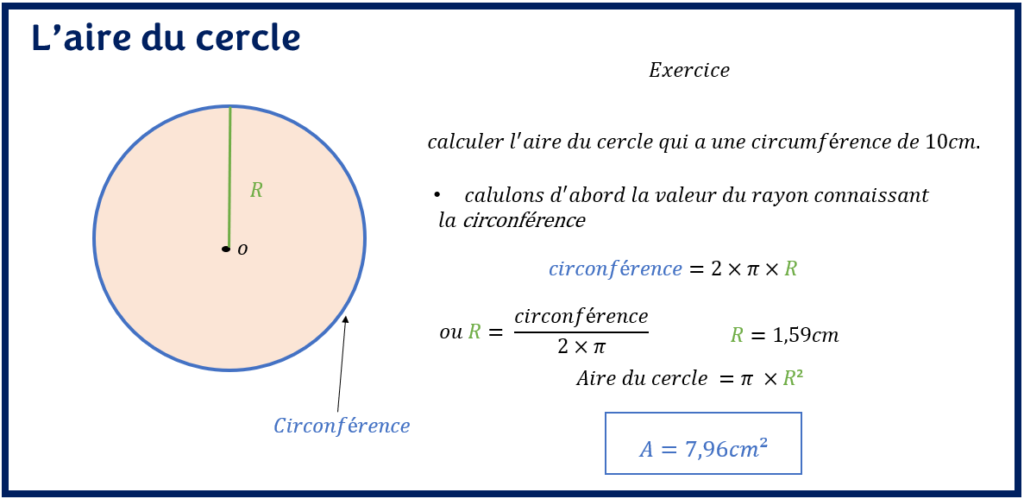
Trouver l’aire d’un cercle est un calcul simple si vous connaissez la mesure du rayon du cercle. Cependant, si ni le rayon ni le diamètre ne sont pas connus, le calcul de la surface du cercle n’est plus si simple. Ici, on verra comment à partir de la circonférence ou du périmètre du cercle, on peut se débrouiller à calculer l’aire d’un cercle.

Dans ce cas, le calcul de l’aire ou la surface du cercle se fait en deux étapes :

• Isoler le rayon ou le diamètre du cercle de la formule de la circonférence du cercle
• Calculer l’aire du cercle en utilisant le rayon ou le diamètre du cercle obtenu

Regardons maintenant comment le mettre en pratique dans un exemple.

Conseils et astuces concernant l’aire d’un cercle

• Un cercle est une figure constituée de tous les points d’un plan à égale distance d’un point donné, le centre.
• La longueur du diamètre d’un cercle est le double de la longueur de son rayon.
• Le diamètre d’un cercle est la corde la plus longue du cercle.
• Un cercle possède une infinité d’axes de symétrie et tous les axes de symétrie passent par les diamètres du cercle.
• Un cercle a un ordre infini de symétrie de rotation autour de son centre.
• Un triangle à l’intérieur d’un cercle qui se compose de deux rayons et de la corde qui les relie est un triangle isocèle.
• Tous les cercles sont semblables : ils ont tous la même forme mais peuvent avoir une taille différente.
• On peut prouver que deux cercles sont superposables si leurs rayons, diamètres ou circonférences sont de même longueur.
• Si des cordes de même longueur relient des rayons dans le même cercle ou dans des cercles superposables, alors les deux triangles isocèles formés par la corde et les rayons sont superposables.

FAQ relative au calcul de l’aire d’un cercle

Sujets similaires

• 
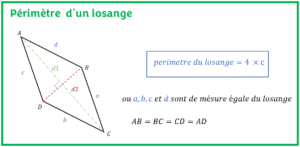
  Périmètre d’un losange
  L’objectif est d’apprendre à calculer le périmètre d’un losange et de connaitre ses propriétés avec des exemples résolus.
• 
  Aire d’un cercle
  L’objectif est d’apprendre comment calculer l’aire d’un cercle et de connaitre ses propriétés avec des exemples résolus.
• 
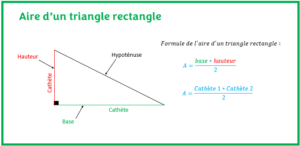
  Aire d’un triangle rectangle
  L’objectif est d’apprendre comment calculer l’aire d’un triangle rectangle de plusieurs façons différentes avec des exercices résolus.
• 
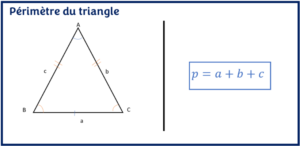
  Périmètre du triangle
  L’objectif est d’apprendre à calculer le périmètre du triangle et de connaître ses propriétés à partir d’exercices résolus.
• 
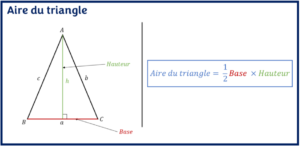
  Aire du triangle
  L’objectif est d’apprendre à calculer l’aire d’un triangle et de connaître ses propriétés à partir d’exercices résolus.
• 
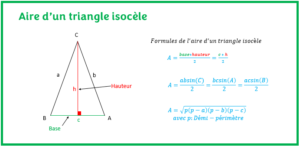
  Aire d’un triangle isocèle
  L’objectif est d’apprendre à calculer l’aire d’un triangle isocèle de plusieurs façons différentes avec des exercices résolus.
• 
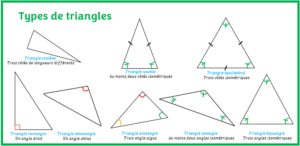
  Les types de triangles
  L’objectif est d’apprendre les différents types de triangles existants et leurs propriétés avec des exemples résolus.
• 
  Périmètre du rectangle
  L’objectif est d’apprendre à calculer le périmètre du rectangle et de connaître ses propriétés à partir d’exercices résolus.