MATRICE AUGMENTÉE

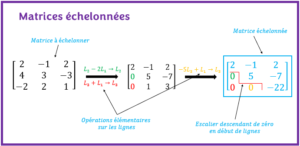
L’objectif est d’apprendre à écrire la matrice augmentée d’un système d’équations et de l’échelonner à l’aide d’exercices résolus.

Sommaire

Rappel et mise en contexte

Plusieurs articles ont déjà été écrits au sujet des matrices. Nous avons vu des opérations élémentaires avec les matrices notamment: l’addition des matrices, la soustraction de matrice, la multiplication de matrice et la transposée d’une matrice, mais aussi des opérations plus avancées à savoir : l’inverse d’une matrice et le déterminant d’une matrice.

Les matrices occupent une grande place dans l’algèbre linéaire et particulièrement dans les systèmes d’équations linéaires. De nombreuses méthodes élémentaires (méthode de comparaison, méthode de substitution et méthode d’élimination) et avancées (méthode de Gauss, méthode de Gauss – Jordan, méthode de la matrice inverse) existent pour résoudre ces systèmes.

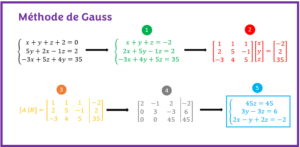
La méthode de Gauss est la méthode populaire pour résoudre les systèmes d’équations. Cette méthode nécessite la construction d’une matrice particulière appelée la matrice augmentée. Cette matrice doit ensuite être échelonner selon la structure suivante :

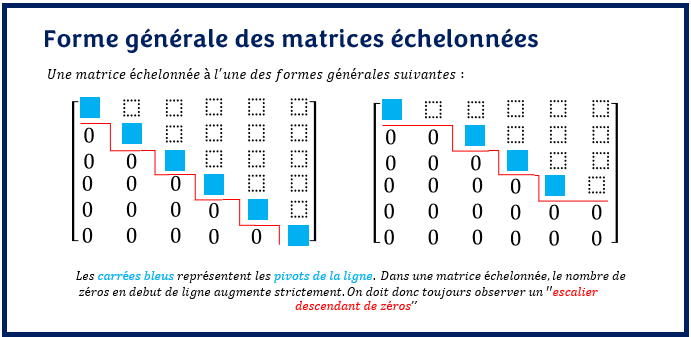
Dans cet article, nous nous intéresserons à la matrice augmentée d’un système.

Systèmes d’équations linéaires et la matrice augmentée

Un système d’équations linéaires est un ensemble de plusieurs équations linéaires à résoudre simultanément. Un système peut être transformer sous une forme matriciel plus simple permettant ainsi d’utiliser les concepts de matrices et leurs propriétés.

La matrice augmentée est une forme synthétique d’un système d’équations et contient toute l’information nécessaire pour le comprendre et le résoudre.

Comment passer d’un système d’équations à la matrice augmentée

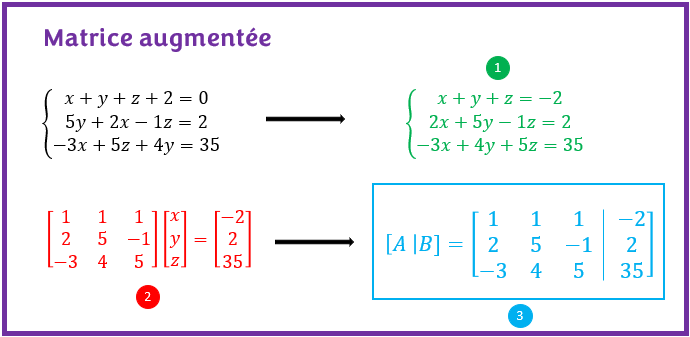
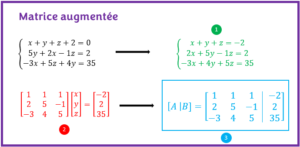
La matrice augmentée d’un système s’obtient à partir d’un système d’équations linéaires en respectant les étapes suivantes :

• Ordonner chaque équation du système d’équations sous la forme générale d’une équation linéaire : a₁x₁ + a₂x₂ + a₃x₃ + … + a_nx_n = b où, a₁, a₂, a₃, …, a_n sont les coefficients respectifs des variables x₁, x₂, x₃, …, x_n et b est une constante.
• Transformer le système d’équations sous la forme AX=B où A est la matrice contenant tous les coefficients des variables du système et B est la matrice contenant toutes les constantes du système.
• Construire la matrice augmentée [A|B] à partir des matrices A et B obtenues à l’étape 2

Ordonner les équations du système sous la forme générale d’une équation linéaire

La première étape de l’obtention de la matrice augmentée d’un système consiste à réarranger les équations du système pour avoir le même ordre d’apparition des variables dans chaque équation. Cet étape sert juste à faciliter l’étape suivante qui est de transformer la matrice sous la forme AX=B.

Dans les exemples suivants, ordonner les équations du système sous la forme générale d’une équation linéaire

Comme vous l’avez constaté, cet étape est simple et élémentaire. Il faut juste se rappeler de changer le signe de chaque terme qui traverse l’égalité de l’équation.

Transformer le système d’équations sous la forme AX=B

Un article complet permettant de transformer un système sous la forme AX=B a déjà été écrit. Ceci est donc un rappel de tout ce qui avait déjà été vus. Mettre un système sous la forme AX=B demande d’anticiper la taille des matrices A, X et B.

La matrice A est de taille m x n où m est le nombre de lignes de la matrice correspondant aux nombres d’équations du système et n est le nombre de colonnes de la matrice correspondant aux nombres de variables du système. La première colonne de la matrice A contient tous les coefficients de la première variable du système et la dernière colonne de la matrice A contient tous les coefficients de la dernière variable du système. Similairement, la première ligne de la matrice A contient tous les coefficients de toutes les variables de la première équation et la dernière ligne de la matrice contient tous les coefficients de toutes les variables de la dernière équation du système.

La matrice colonne X est de taille m x 1 où m représente le nombre de lignes correspondant au nombre d’équations du système. La colonne de la matrice X contient les variables du système d’équation dans l’ordre d’apparition.

Quant à la matrice B, elle est de dimension m x 1. Elle contient toutes les constantes de chaque équation du système.

Reprenons les deux exemples ci-dessus et transformons les sous la forme AX=B.

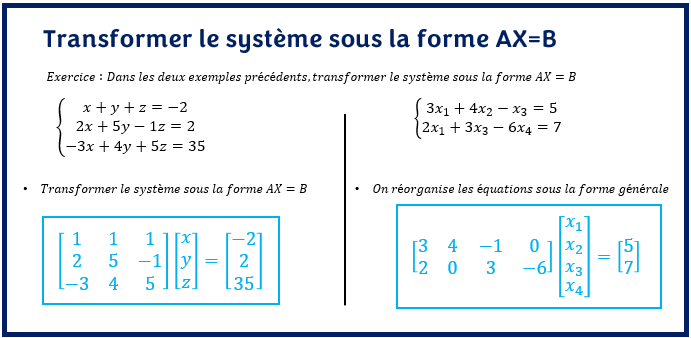
Relisez les caractéristiques des matrices A, X et B précédents et validez que les résultats obtenus sont logiques et cohérents.

Construire de la matrice augmentée [A|B] du système

La matrice augmentée du système s’obtient en combinant les matrices A et B obtenue précédemment. Elle se note [A|B], car on ajoute une colonne de plus à la matrice A. Cette colonne est la matrice B. En gros, si la matrice A a 3 colonnes, la matrice [A|B] en aura 4.

Reprenons les deux exemples précédents et construisons les matrices augmentées de ces systèmes:

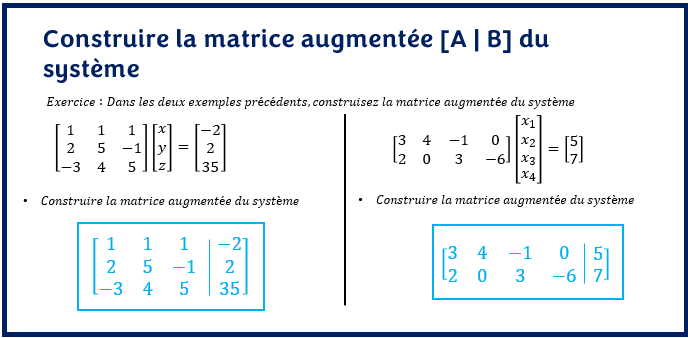
Au regard de ces exemples, pouvez-vous anticiper les dimensions de ces matrices ?

Dans le premier exemple, la matrice [A|B] a 3 lignes et 4 colonnes, car le système d’équations a trois équations et 3 variables. Dans le deuxième exemple, la matrice [A|B] est de dimension 2×5, car le système d’équations a 2 équations et 4 variables.

Dimension de la matrice augmentée d’un système

Soit un système d’équation sous la forme AX=B où m représente le nombre de lignes et n le nombre de colonnes de la matrice A. Les matrices suivantes les dimensions suivantes :

• A est de dimension m x n : A_mxn
• X est de dimension _{n x 1} : X_nx1
• B de dimension m x 1 : B_mx1
• La matrice augmentée [A|B] est de dimension m x (n+1) : cette matrice a toujours une colonne de plus que la matrice A mais le même nombre de lignes.

Comment échelonner la matrice augmentée d’un système?

La matrice augmentée d’un système s’échelonne même manière que toutes les autres matrices en respectant les opérations élémentaires sur les lignes. Dans l’article sur les matrices échelonnées, nous avons expliqué étapes par étapes comment échelonner une matrice. Dans cette section, nous faisons juste un bref rappel.

Opérations élémentaires sur les lignes de la matrice augmentée

Trois opérations élémentaires sont utilisées pour échelonner une matrice augmentée :

• permuter les lignes de la matrice ( L_i ↔ L_j ), c’est-à-dire ( L_i → L_j ) et ( L_j → L_i ).
• multiplier une ligne par une constante k, où k ∈ ℝ et k ≠ 0 : ( kL_i ↔ L_i),
• Additionner un multiple k (k ∈ ℝ) d’une ligne à une autre ligne ( L_i + kL_j→ L_i )

On peut également combiner ces opérations en une seule étape. Par exemple, en effectuant les opérations 2) et 3) précédentes simultanément sur les lignes L_i et L_j, nous obtenons k₁L_i + k₂L_j → L_i, où k₁ ≠ 0.

Aucune opération élémentaire n’est possible sur les colonnes de la matrice.

Échelonner la matrice augmentée du système

Pour échelonner la matrice augmentée, il faut suivre les étapes suivantes :

• S’assurer que le premier élément (élément a₁₁) de la première ligne de la matrice est non nul. C’est le pivot de la première ligne. S’il est nul, effectuer d’abord une permutation de lignes avec les lignes en dessous.
• Se servir de ce pivot pour transformer tous les autres chiffres en dessous de lui en des zéros en utilisant la troisième opération élémentaire ( L_i + kL_j→ L_i ) ou une combinaison des opérations 2 et 3. L_i représente la ligne à modifier et L_j représente la ligne du pivot.
• Recommencer les étapes 1 et 2 avec la deuxième ligne et ainsi de suite jusqu’à ce qu’il ne reste plus de lignes

Essayons d’appliquer les étapes ci-dessus pour échelonner les matrices augmentées des exemples précédents.

Il est important l’effectuer l’opération de changement de lignes sur toutes la ligne de la matrice. Le trait verticale à l’avant dernière colonne représente la séparation entre la matrice A et la matrice B. La matrice augmentée doit être traité comme une seule matrice sans ternir compte du trait verticale.

Rang de la matrice augmentée

Soit A une matrice. Le rang de la matrice est égal au nombre de pivot de la matrice A. On note rang(A). Pour trouver le rang d’une matrice, il faut d’abord l’échelonner. Par conséquent, le rang de la matrice augmentée est donc égal à son nombre de pivots une fois échelonnée.

Le rang d’une matrice est toujours plus petit ou égal au nombre le plus petit entre le nombre de ligne et le nombre de colonne de la matrice. Si la matrice A est de dimension mxn, alors rang(A) < min (m, n).

Considérons un système d’équations sous la forme AX=B. On sait que la matrice augmentée a toujours plus de colonne que de lignes par conséquent, son rang sera toujours plus petit ou égale à son nombre de lignes.

Les pivots de la matrice A sont toujours les mêmes que ceux de la matrice augmentée [A|B]. Par conséquent, le rang de la matrice A est toujours égale au rang de la matrice augmentée : rang(A) = rang ( [A|B] ).

Conseils et astuces

• À chaque système d’équations linéaires est associé une matrice augmentée
• La matrice augmentée d’un système utilise les matrices A et B du système lorsqu’il est sous la forme AX=B.
• Ne pas oublier d’ordonner les équations du système avant de la transformer sous la forme AX=B
• La matrice augmentée d’un système a toujours une colonne de plus que la matrice A
• Le nombre de ligne de la matrice A est égale au nombre d’équations du système et son nombre de colonne est égale au nombre de variables ou inconnues
• La matrice B a une seule colonne et a le même nombre de ligne que le nombre d’équations du système
• La matrice X est une matrice colonne donc le nombre de lignes est égale au nombre d’inconnues du système
• La matrice augmentée s’échelonne de la même manière que toutes autres matrices
• Le rang de la matrice augmentée est toujours plus petit ou égal à son nombre de lignes
• Les pivots de la matrice A sont toujours aussi les pivots de la matrice augmentée
• Le rang de la matrice augmentée est toujours égale au rang de la matrice A
• Utiliser Symbolab pour effectuer vos calculs matriciels
• Demander l’assistance d’un tuteur au besoin

FAQ

Sujets similaires

• 
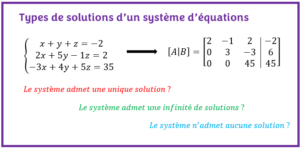
  COMMENT SAVOIR SI UN SYSTÈME ADMET UNE SOLUTION
  Découvrez les trois types de solutions d’un système. Apprenez comment savoir si un système admet des solutions avec des exercices résolus.
• 
  MÉTHODE DE GAUSS
  L’objectif est d’apprendre à résoudre un système d’équations linéaires par la méthode de Gauss à partir d’exercices résolus.
• 
  MATRICE AUGMENTÉE
  L’objectif est d’apprendre à écrire la matrice augmentée d’un système d’équations et de l’échelonner à l’aide d’exercices résolus.
• 
  MATRICES ÉCHELONNÉES
  L’objectif est d’apprendre à échelonner une matrice et à reconnaître les matrices échelonnées à l’aide d’exercices résolus.
• 
  FORME AX=B : TRANSFORMER UN SYSTÈME D’ÉQUATIONS LINÉAIRES
  L’objectif est d’apprendre comment transformer un système d’équations linéaires sous la forme AX=B avec des exercices résolus.
• 
  MÉTHODE PAR ÉLIMINATION
  L’objectif est d’apprendre à résoudre un système d’équations linéaires par la méthode d’élimination avec des exercices résolus.
• 
  MÉTHODE DE SUBSTITUTION
  L’objectif est d’apprendre à résoudre un système d’équations linéaires par la méthode de substitution avec des exercices résolus.
• 
  MÉTHODE DE COMPARAISON
  L’objectif est d’apprendre à résoudre un système d’équations linéaires par la méthode de comparaison avec des exercices résolus.