L’objectif est d’apprendre à calculer le périmètre du triangle et de connaître ses propriétés à partir d’exercices résolus.
Sommaire
Rappel et mise en contexte
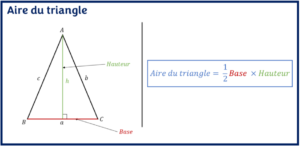
Un triangle est une figure géométrique à trois côtés et trois angles. La somme des angles dans un triangle est toujours de 180 degrés. Aussi, dans un triangle, le côté ayant la mesure la plus grande est toujours opposé à l’angle le plus grand. Similairement, le côté ayant la mesure la plus petite est toujours opposé à l’angle le plus petit du triangle.
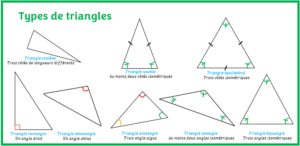
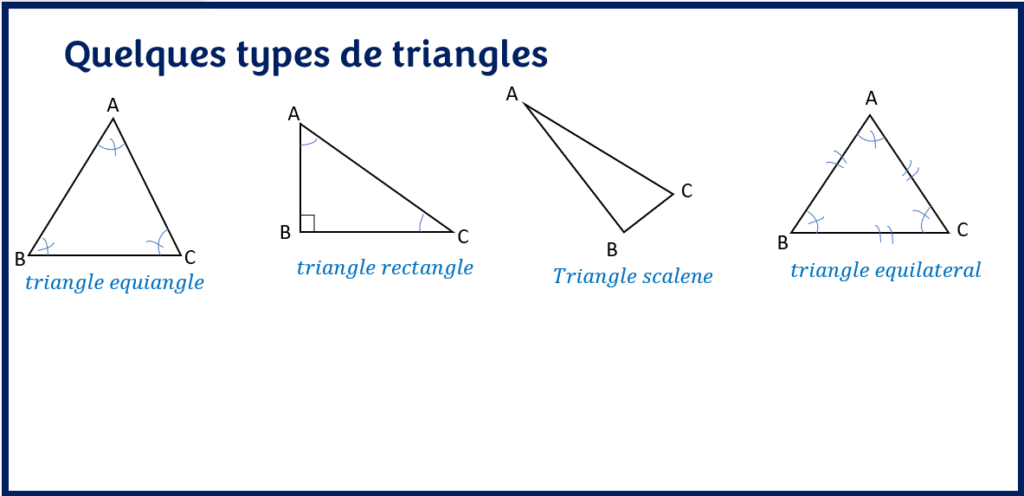
Il existe plusieurs types de triangles dont les plus importants sont : le triangle isocèle, le triangle équilatérale, le triangle rectangle. Il est souvent nécessaire de calculer la mesure des côtés manquants du triangle avant de calculer le périmètre. Dans ces cas, on peut se servir des nombreuses relations mathématiques dans les triangles que nous avons déjà discutés dans les articles précédents. On peut citer la relation de Pythagore, les rapports trigonométriques, la loi des sinus et la loi des cosinus.
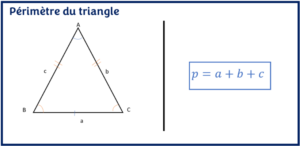
Le périmètre du triangle représente la longueur de la ligne qui délimite les contours du triangle. Mathématiquement, le périmètre du triangle est la somme de tous les cotés du triangle. Quelque soit le type de triangle, le principe de calcul du périmètre est le même.
Nous verrons dans les lignes suivantes comment calculer le périmètre de ces différents triangle ainsi que leurs spécificité.
Calcul du périmètre du triangle
Calcul du périmètre d’un triangle rectangle
Un triangle rectangle est un triangle qui possède un angle droit égale à 90 degrés. Le côté le plus long du triangle rectangle est appelée hypoténuse. Il est toujours opposé à l’angle droit. Les deux autres cotés du triangle sont appelé cathètes. Les cathètes n’ont pas forcément la même longueur. Lorsque les cathètes sont égales, le triangle est dit triangle rectangle isocèles.
La formule du périmètre du triangle rectangle est :
P = somme de tous les côtés
Où, P : périmètre du triangle
La recherche des mesures manquantes pour calculer le périmètre d’un triangle rectangle se fait principalement à l’aide de la relation de Pythagore, les rapports trigonométriques et les relations métriques. Regardons maintenant les deux exemples ci-dessous :
Périmètre du triangle rectangle en utilisant les rapports trigonométriques
Comment calculer le périmètre du triangle rectangle dans l’exercice ci-dessous :
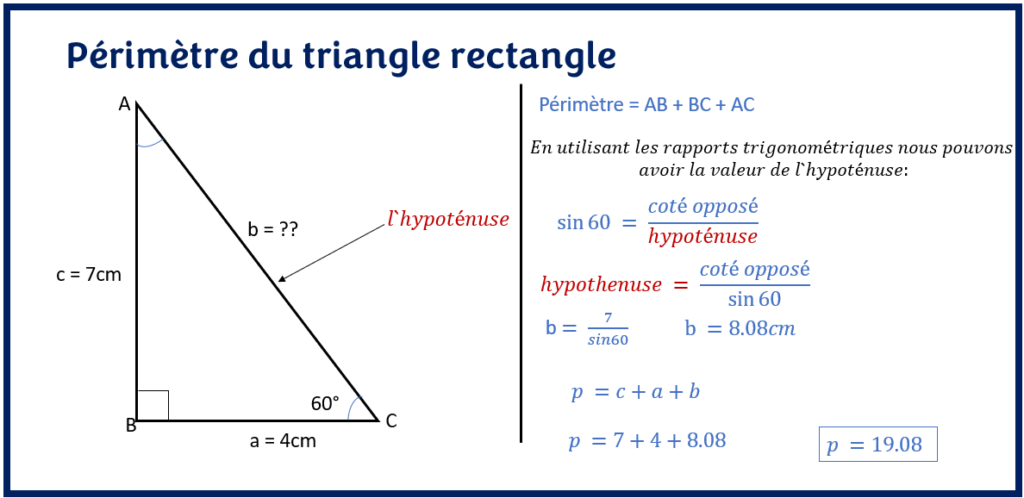
Avant de calculer le périmètre du triangle rectangle, la première chose à valider est de se rassurer que tous les côtés du triangle ont la même unité. Si les côtés ne sont pas à la même unité, il faudra les convertir en une unité commune.
Dans l’exemple ci-dessous, on voit bien qu’on a pu obtenir la mesure de l’hypoténuse du triangle en utilisant les rapports trigonométriques (SOH-CAH-TOA) puisqu’on connait un angle du triangle. Ensuite, on peut obtenir le périmètre du triangle en additionnant tous ces côtés.
Périmètre du triangle rectangle en utilisant la relation de Pythagore
Vous l’avez remarquez, dans l’exemple précédents, on aurait pu directement directement la mesure de l’hypoténuse en utilisant le théorème de Pythagore. Il est utilisé lorsqu’on a la mesure des deux autres côtés du triangles.
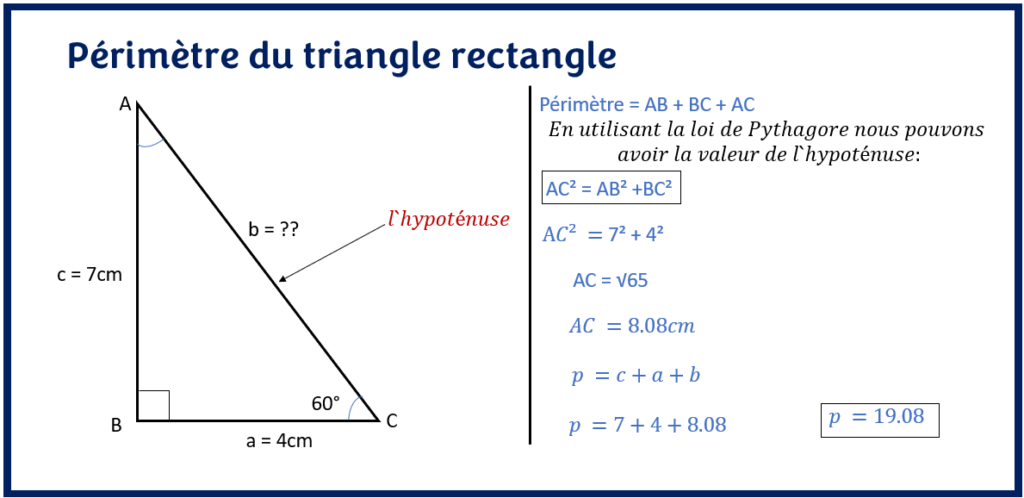
On obtient bien évidemment le même résultat que précédemment mais en utilisant une autre méthode
Calcul du périmètre du triangle isocèle
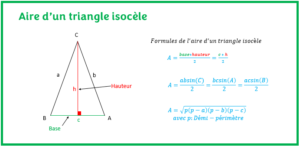
On appelle triangle isocèle tout triangle qui possède deux côtés égaux ou alors deux angles égaux. Pour un triangle isocèle, la hauteur issue de son sommet principale divise le côté qui lui est opposé en deux parties égales. Cette hauteur issue du somment principal représente aussi l’axe de symétrie du triangle et la médiatrice du côté qui lui est opposé.
Le calcul du périmètre pour ce type de triangle nécessite donc juste la connaissance de deux côtés du triangle distincts.
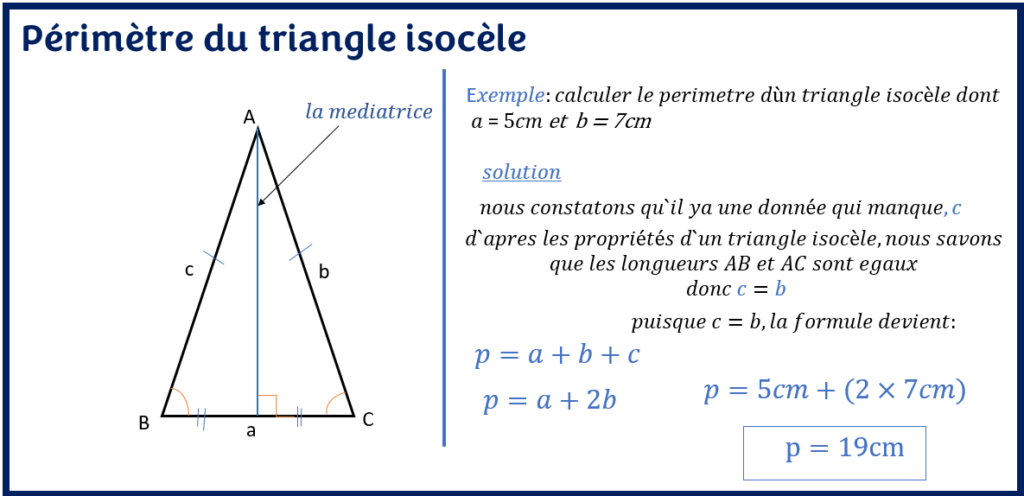
En gros, puisque un triangle isocèle a deux coté égaux, la formule du périmètre pour un triangle isocèle devient :
P = a +2b
Où P : périmètre, a : base du triangle, b : mesure des côtés égaux.
Lorsqu’un angle du triangle isocèle est connu, on peut utiliser les rapports trigonométriques, la loi de cosinus et de la loi des sinus pour déterminer la mesure du coté manquant. Vous pouvez consulter l’article précédent concernant l’aire d’un triangle isocèle afin de voir comment utiliser ces relations mathématiques.
Calcul du périmètre du triangle équilatéral
Le triangle équilatéral fait partie des types de triangles les plus importants. Il se caractérise par le fait que tous ses côtés sont égaux. De ce fait, tous les angles du triangle équilatéral sont aussi égaux.
Le calcul du périmètre du triangle équilatéral est donc encore plus simple. Il suffit de connaître la mesure d’un côté du triangle et de le multiplier par 3 (addition de trois mesures égales).
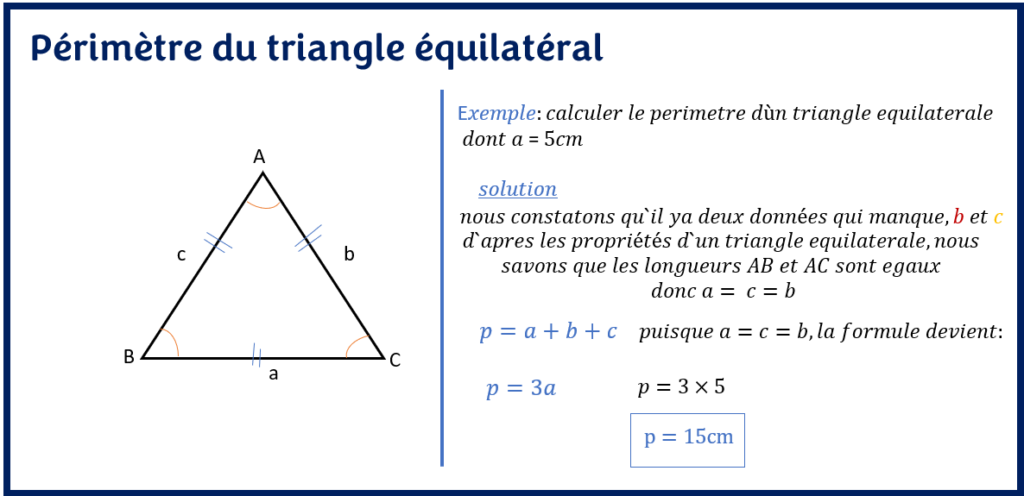
On peut également utiliser tous les outils mathématiques que nous avons déjà présenté ci-dessus pour calculer une mesure manquante. Toutes les propriétés de triangle équilatéral se trouve dans l’article sur les types de triangles
Calcul du périmètre du triangle scalène ou triangle quelconque
Un triangle scalène est un triangle qui a trois côtés de longueurs différentes et trois angles de mesures différentes. On parle aussi de triangle quelconque. Les propriétés d’un triangle quelconque sont les propriétés générales à tous les triangles.
Pour le calcul du périmètre, il faut donc connaitre la mesure de chacun des côtés distincts. Pour ce type de triangle, la recherche d’une mesure manquante passe nécessairement par la loi des sinus ou la loi des cosinus.
La formule du périmètre d’un triangle quelconque est donc :
P = a + b + c
Où, P : périmètre, a, b, c: côté du triangle scalène.
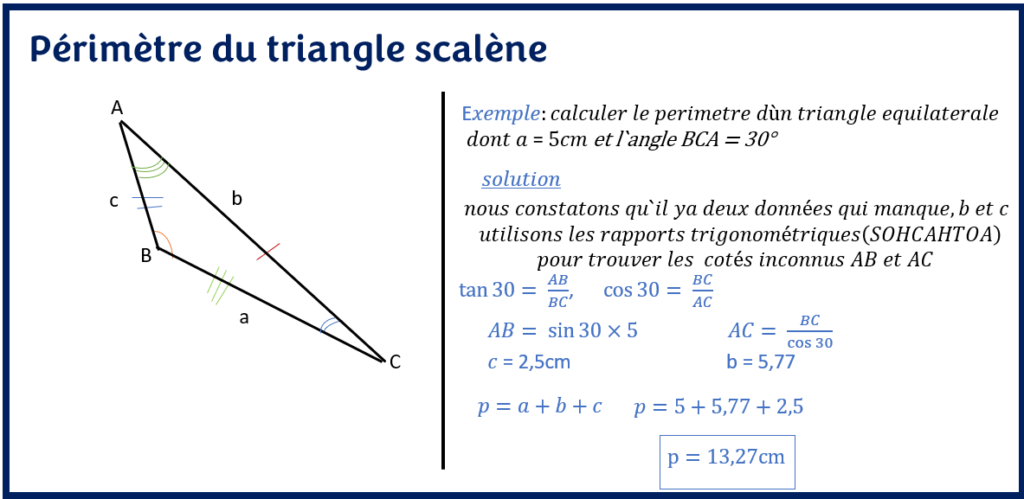
Les propriétés du triangle scalène sont dans l’article sur les types de triangles.
Conseils et astuces concernant le périmètre du triangle
- Le périmètre d’un triangle est la somme de tous ses côtés
- Pour calculer une mesure manquantes dans un triangle, on peut utiliser les relations suivantes: la relation de Pythagore, les relation métriques, les rapports trigonométriques, la loi des sinus, la loi des cosinus et les triangles semblables.
- Le périmètre d’un triangle peut aussi être obtenu à partir de son aire.
- La somme des angles dans un triangle est toujours de 180 degrés
- Pour un triangle rectangle, le coté le plus grand est appelé l`hypoténuse. Il est toujours opposé à l’angle droit.
- Un triangle isocèle a toujours deux cotés égaux et deux angles égaux
- Tous les trois cotés du triangle équilatéral sont égaux. Il en est de même pour ses angles (égaux à 60 degrés chacun)
- Consulter la vidéo explicative du périmètre du triangle au besoin.
FAQ
Pour calculer l’aire d’un triangle avec le périmètre, on peut utiliser la formule de Héron si l’on connait toutes les autres mesures des côtés du triangles.
Généralement, la connaissance du périmètre peut permettre de déterminer la mesure des autres côtés manquants du triangle permettant de calculer son aire ou sa surface.
Quelque soit le type de triangle, le périmètre est la somme de tous les côtés. Des particularités se situent dans le calcul des mesures manquants des côtés du triangle. Dans ces cas, il est très important de connaitre les propriétés du triangle à l’étude et les règles de calcul dans les triangles.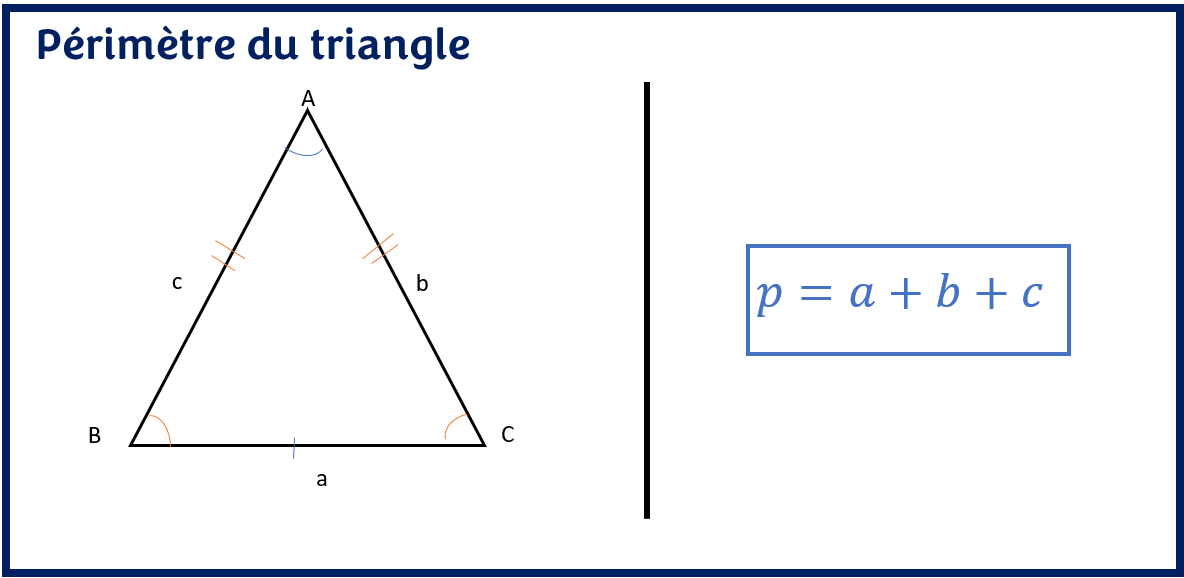
Pour calculer la longueur du troisième côté d’un triangle, on peut utiliser des techniques de calculs suivantes : la relation de Pythagore, les rapports trigonométriques, les lois de cosinus et la loi des sinus. Tous ces méthodes de calculs se trouve dans les articles précendents.
Sujets similaires
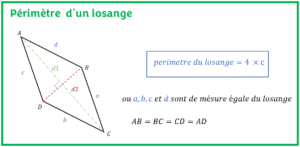
- Périmètre d’un losangeL’objectif est d’apprendre à calculer le périmètre d’un losange et de connaitre ses propriétés avec des exemples résolus.
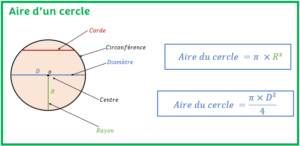
- Aire d’un cercleL’objectif est d’apprendre comment calculer l’aire d’un cercle et de connaitre ses propriétés avec des exemples résolus.
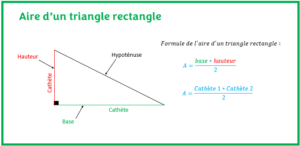
- Aire d’un triangle rectangleL’objectif est d’apprendre comment calculer l’aire d’un triangle rectangle de plusieurs façons différentes avec des exercices résolus.
- Périmètre du triangleL’objectif est d’apprendre à calculer le périmètre du triangle et de connaître ses propriétés à partir d’exercices résolus.
- Aire du triangleL’objectif est d’apprendre à calculer l’aire d’un triangle et de connaître ses propriétés à partir d’exercices résolus.
- Aire d’un triangle isocèleL’objectif est d’apprendre à calculer l’aire d’un triangle isocèle de plusieurs façons différentes avec des exercices résolus.
- Les types de trianglesL’objectif est d’apprendre les différents types de triangles existants et leurs propriétés avec des exemples résolus.
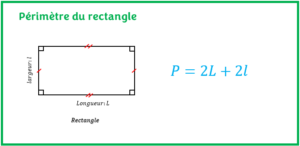
- Périmètre du rectangleL’objectif est d’apprendre à calculer le périmètre du rectangle et de connaître ses propriétés à partir d’exercices résolus.