L’objectif est d’apprendre à utiliser les relations métriques dans un triangle rectangle pour déterminer une mesure manquante à partir d’exercices résolus.
Sommaire
Rappel et mise en contexte
Le triangle rectangle est l’une des figures géométriques(carré, rectangle, cercle, trapèze, polygone) les plus utilisées en géométrie. Jusqu’à présent, de nombreuses formules ont été développées pour ce type de triangle notamment la relation de Pythagore, les relations métriques, les formules de trigonométries (SOH-CAH-TOA) et bien d’autres.
Trois relations métriques dans le triangle rectangle permettent de déterminer les dimensions manquantes. Pour commencer, il est important de considérer la hauteur issue de l’angle droit du triangle rectangle. Cette hauteur permet d’obtenir ainsi trois triangles rectangles distincts et semblables selon la condition minimale AA.
Relations métriques: Étapes préliminaires
Afin d’utiliser les relations métriques dans un triangle rectangle pour déterminer des dimensions manquantes, il est d’abord important d’identifier l’hypoténuse du triangle rectangle principale et la hauteur issue de son angle droit.
Ensuite, attribuez les lettres(h, c, a, b, pa, pb) à chaque côté du triangle où:
- h : corresponds à la hauteur du triangle rectangle issue de l’angle droit
- c : corresponds à l’hypoténuse du triangle principale
- a ou b : corresponds aux cathètes du triangle rectangle principal
- pa ou pb : corresponds aux portion du côté a ou b sur l’hypoténuse respectivement (projection de la cathète a ou b sur l’hypoténuse)
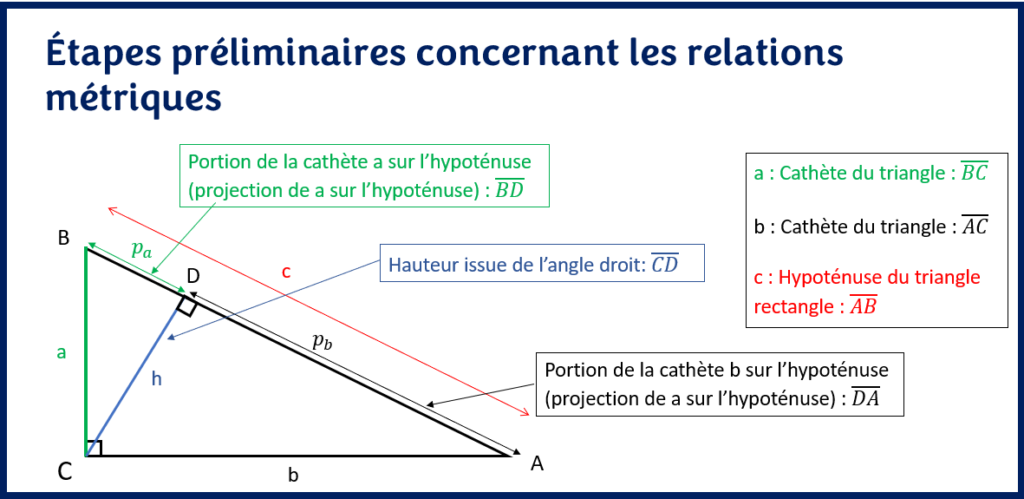
Enfin, il faudra déterminer laquelle des trois relations métriques sera nécessaire pour résoudre le problème.
En plus, comme déjà mentionnée plus haut, la hauteur issue de l’angle droit divise le triangle rectangle ABC en trois triangles rectangles distincts:
- Le triangle CBD rectangle en D
- Le triangle CDA rectangle en D
- Le triangle rectangle ABC rectangle en C
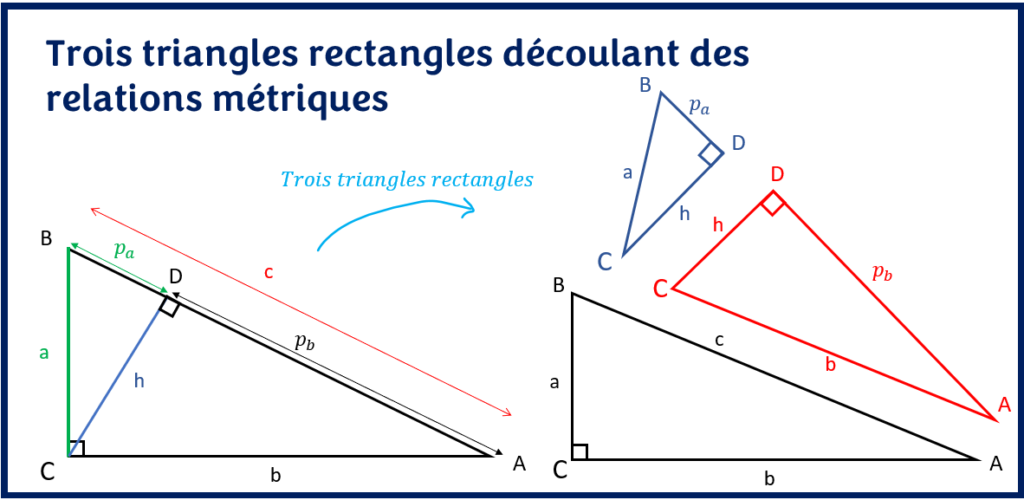
Une fois de plus, la relation de Pythagore sert à déterminer une dimension manquante dans un triangle rectangle. On pourrait donc utiliser cette relation dans chacun de ces trois triangles rectangles.
Sans tarder, nous allons voir un nouvel outil à utiliser dans un triangle rectangle : les relations métriques.
Relations métriques: Théorème de la cathète (1ère relation métrique)
Le théorème de la cathète s’énonce comme suit:
<< Dans un triangle rectangle, la mesure de chaque cathète est la moyenne proportionnelle entre la mesure de sa projection sur l’hypoténuse et la mesure de l’hypoténuse >>
Autrement dit, le théorème de la cathète s’écrit à partir de l’équation suivante:
a2 = pa * c ou b2 = pb * c
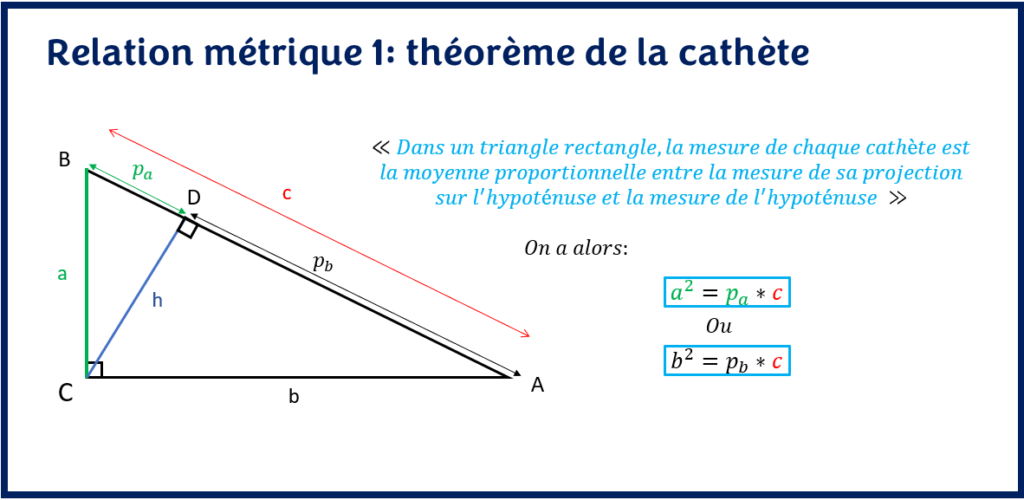
On comprend donc l’importance de savoir identifier l’hypoténuse, la hauteur relative à l’angle droit et les cathètes.
Calcul d’une mesure manquante avec le théorème de la cathète
En ce moment, nous allons voir comment nous pouvons calculer la mesure des côtés manquants d’un triangle rectangle avec le théorème de la cathète(première propriété métrique).
Considérons les deux exemples suivants:
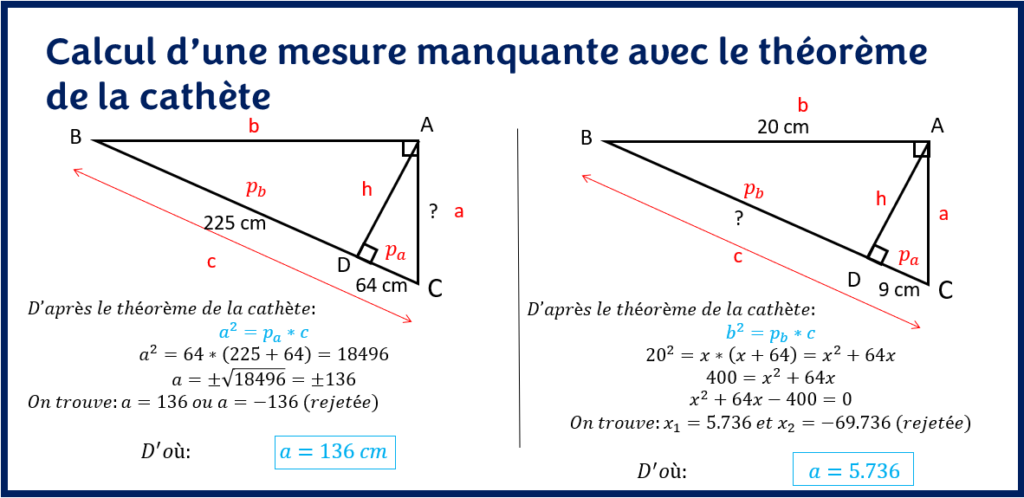
En principe, vous remarquerez que l’utilisation du théorème de la cathète est assez simple. Il suffit de regarder les données de mesures et vérifier s’ils sont suffisants pour utiliser la formule.
Le deuxième exercice est plus complexe que le premier dans ce sens que la mesure de l’hypoténuse n’est pas connue. On aboutit à une équation quadratique qu’on résout par la méthode du discriminant (∆ = b2 – 4ac).
N’oubliez pas que lorsqu’on calcule la racine carrée d’un nombre, on obtient deux solutions (une positive et l’autre négative). On doit donc choisir l’une d’elles et rejeter l’autre.
Relations métriques: théorème de la hauteur relative à l’hypoténuse (2ème relation métrique)
Le théorème de la hauteur relative à l’hypoténuse s’énonce comme suit:
<< Dans un triangle rectangle, la mesure de la hauteur relative à l’hypoténuse est la moyenne proportionnelle entre les mesures des deux segments qu’elle détermine sur l’hypoténuse. >>
En d’autres termes, le théorème de la hauteur relative à l’hypoténuse s’écrit à partir de l’équation suivante:
h2 = pa * pb
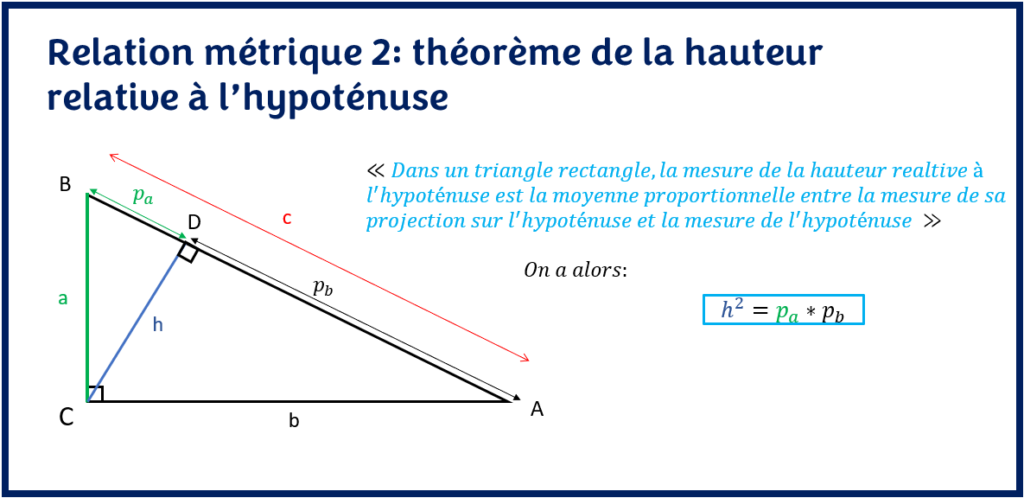
Cette relation métrique permet de calculer la hauteur relative à l’angle droit ou l’une ou l’autre des mesures sur l’hypoténuse AB (pa ou pb).
Encore une fois, pa et pb représente les projections des cathètes a et b sur l’hypoténuse respectivement.
Calcul d’une mesure manquante avec le théorème de la hauteur relative à l’hypoténuse
Regardons maintenant comment utiliser la deuxième relation métrique pour calculer une mesure manquante.
Considérons les deux exemples suivants:
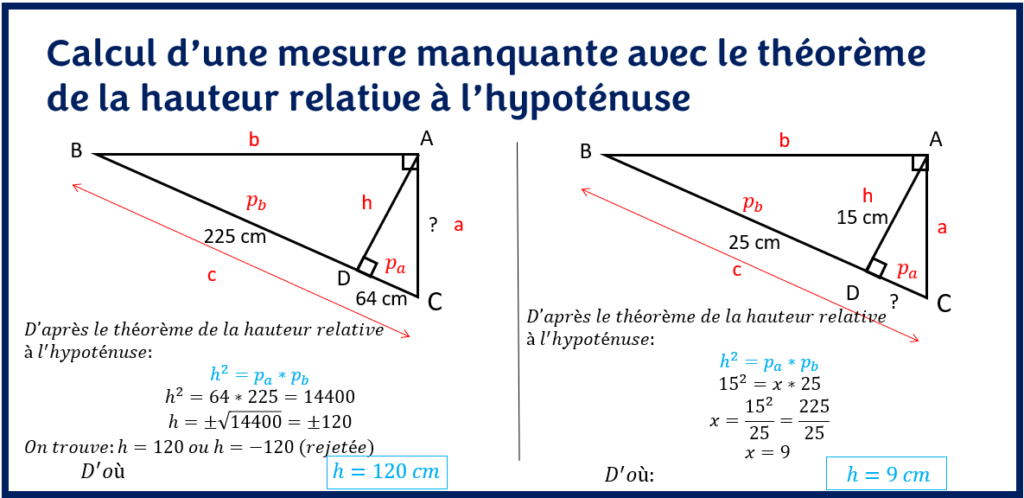
La deuxième relation métrique présente une similarité avec la première en ce qui concerne l’expression et la facilité d’utilisation. Une fois de plus, on regarde les mesures données dans le problème et l’on applique la formule la plus appropriée. On marque par x la mesure manquante au moment de remplacer les valeurs des longueurs dans la formule pour le calcul et l’on résout l’équation.
Relations métriques: théorème du produit des cathètes (3ème relation métrique)
Le théorème du produit des cathètes s’énonce alors comme suit:
<< Dans un triangle rectangle, le produit des mesures des cathètes est égal au produit des mesures de l’hypoténuse et de la hauteur correspondante. >>
Pour ainsi dire, le théorème du produit des cathètes correspond à l’équation suivante:
a * b = c * h
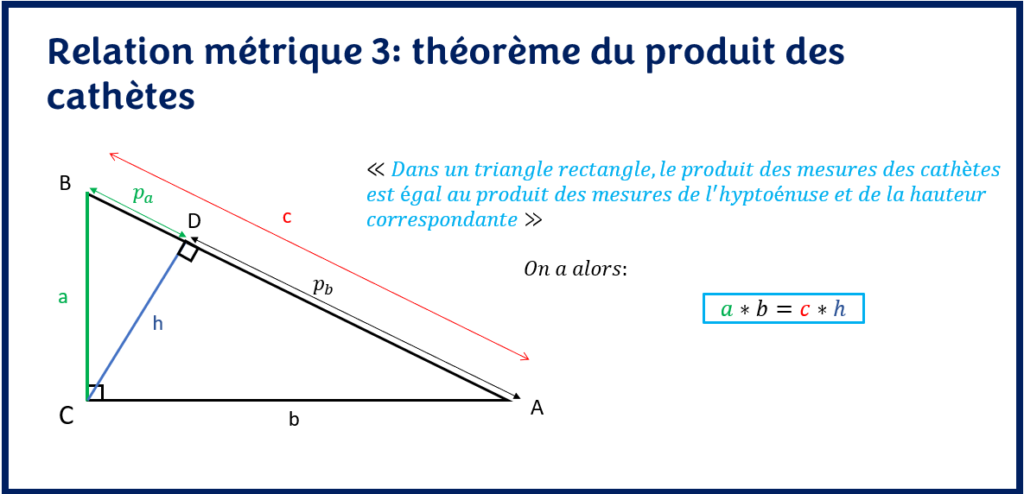
Cette relation métrique utilise tous les côtés du triangle y compris la hauteur relative à l’hypoténuse. Pour tout dire, elle est assez simple à retenir et à utiliser. Il faut avoir trois mesures parmi les quatre pour obtenir la dernière mesure manquante.
Calcul d’une mesure manquante avec le théorème du produit des cathètes
Apprenons dans cette partie comment utiliser la troisième relation métrique pour calculer une mesure manquante avec le théorème du produit des cathètes.
Considérons les deux exemples suivants:
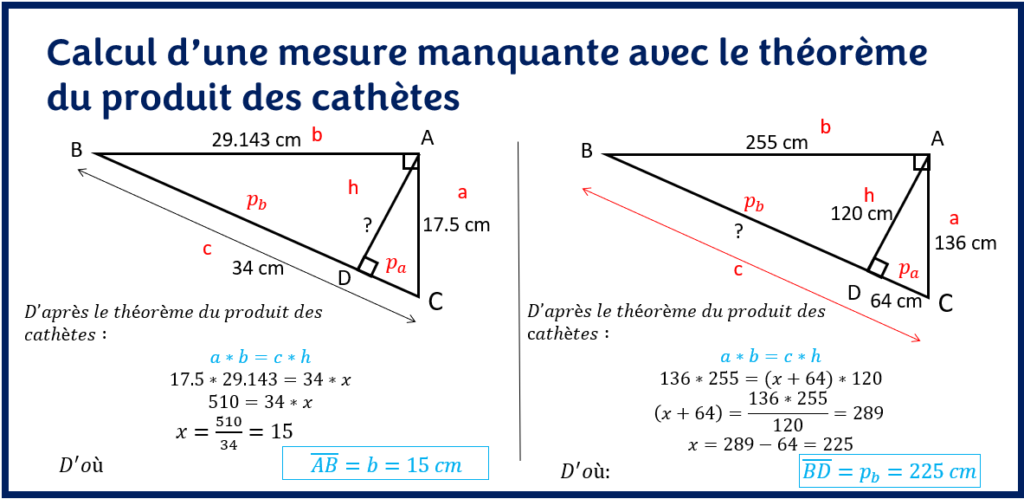
Prenons le cas de l’exemple un, il est facile de constater que l’on connait déjà trois mesures sur quatre. La troisième relation métrique nous aide donc à calculer la hauteur.
Le deuxième exemple est particulier, le théorème du produit des cathètes a juste été utilisé pour démontrer son utilisation. En situation d’examen, il aurait été plus simple d’appliquer la relation de Pythagore dans le triangle ABD rectangle en D ou même d’utiliser la deuxième relation métrique(théorème de la hauteur relative à l’hypoténuse).
Dans le premier exemple, il serait impossible de calculer la mesure de la hauteur AD en une seule opération sans utiliser la troisième relation métrique.
Conseils et astuces concernant les relations métriques
- Les relations métriques sont utilisées uniquement dans un triangle rectangle comprenant une hauteur relative issue de l’angle droit
- Il est nécessaire d’identifier les mesures de côtés du triangle par des lettres a, b, c ,pa , pb selon les définitions présentées dans les étapes préliminaires
- Il ne faut pas oublier l’utilisation de la relation de Pythagore pour déterminer des mesures manquantes
- Consulter la vidéo explicative sur les relations métriques dans un triangle rectangle
- Si vous ne comprenez toujours pas après la lecture de ce cours, vous pouvez demander l’assistance d’un tuteur en ligne en écrivant par courriel.
FAQ en rapport avec les relations métriques
Il existe 3 relations métriques dans un triangle rectangle:
– Première relation métrique : Théorème de la cathète
– Deuxième relation métrique : Théorème de la hauteur relative à l’hypoténuse
– troisième relation métrique : Théorème du produit des cathètes 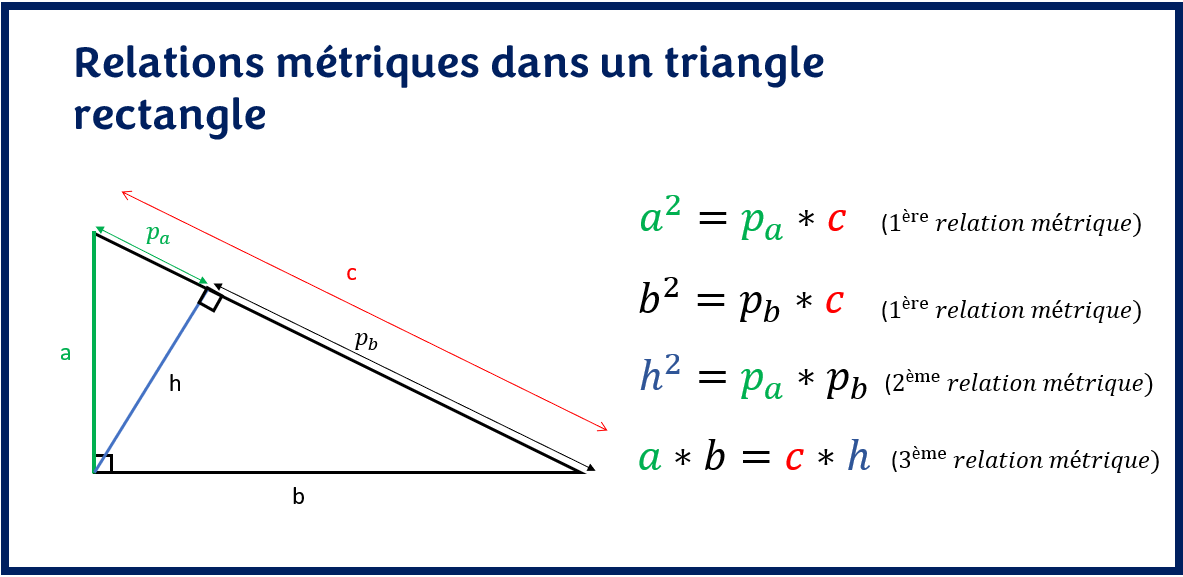
Il existe plusieurs façons de calculer une cathète. Dans un triangle rectangle par exemple, on pourrait utiliser les relations métriques ou même la relation de Pythagore. On pourrait également utiliser des formules trigonométriques.
Pour calculer l’hypoténuse, la relation de Pythagore peut être utilisée. Les relations métriques dans le triangle rectangle sont également une alternative dans le cas où l’on a la hauteur relative à l’hypoténuse. Pour en savoir plus sur ces deux relations, vous pouvez consulter le cours sur la relation de Pythagore ou le cours sur les relations métriques dans un triangle rectangle.
Sujets similaires
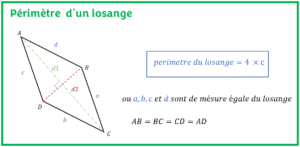
- Périmètre d’un losangeL’objectif est d’apprendre à calculer le périmètre d’un losange et de connaitre ses propriétés avec des exemples résolus.
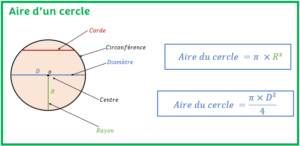
- Aire d’un cercleL’objectif est d’apprendre comment calculer l’aire d’un cercle et de connaitre ses propriétés avec des exemples résolus.
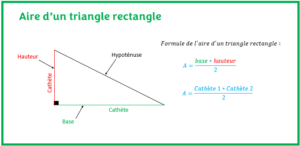
- Aire d’un triangle rectangleL’objectif est d’apprendre comment calculer l’aire d’un triangle rectangle de plusieurs façons différentes avec des exercices résolus.
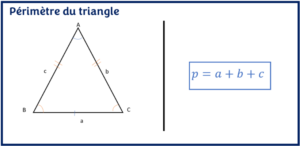
- Périmètre du triangleL’objectif est d’apprendre à calculer le périmètre du triangle et de connaître ses propriétés à partir d’exercices résolus.
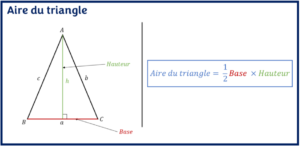
- Aire du triangleL’objectif est d’apprendre à calculer l’aire d’un triangle et de connaître ses propriétés à partir d’exercices résolus.
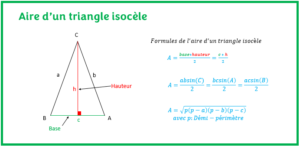
- Aire d’un triangle isocèleL’objectif est d’apprendre à calculer l’aire d’un triangle isocèle de plusieurs façons différentes avec des exercices résolus.
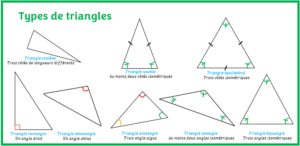
- Les types de trianglesL’objectif est d’apprendre les différents types de triangles existants et leurs propriétés avec des exemples résolus.
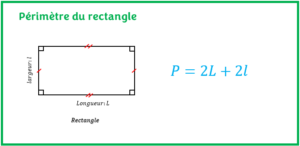
- Périmètre du rectangleL’objectif est d’apprendre à calculer le périmètre du rectangle et de connaître ses propriétés à partir d’exercices résolus.