L’objectif est d’apprendre à appliquer le théorème de Pythagore ou la relation de Pythagore dans un triangle rectangle à partir d’exercices résolus.
Sommaire
Rappel et mise en contexte
De nombreuses formules et propriétés s’appliquent aux figures géométriques. Antérieurement, nous avons présenté dans les articles précédents les formules d’aires et de périmètres des quadrilatères tels que le carré, le rectangle, le triangle, le trapèze, le cercle et bien d’autres. Pourtant, le calcul d’aire et de périmètre d’une figure géométrique repose sur ses mesures connues.
À ce jour, aucune formule permettant de déterminer une longueur manquante sur une figure n’avait encore été déterminée. En outre, le théorème de Pythagore nous aidera justement dans ce sens. La relation de Pythagore permet de déterminer les mesures manquantes dans un triangle rectangle. Ce théorème n’est pas le seul. Les relations métriques peuvent aussi être utilisées.
Triangle rectangle
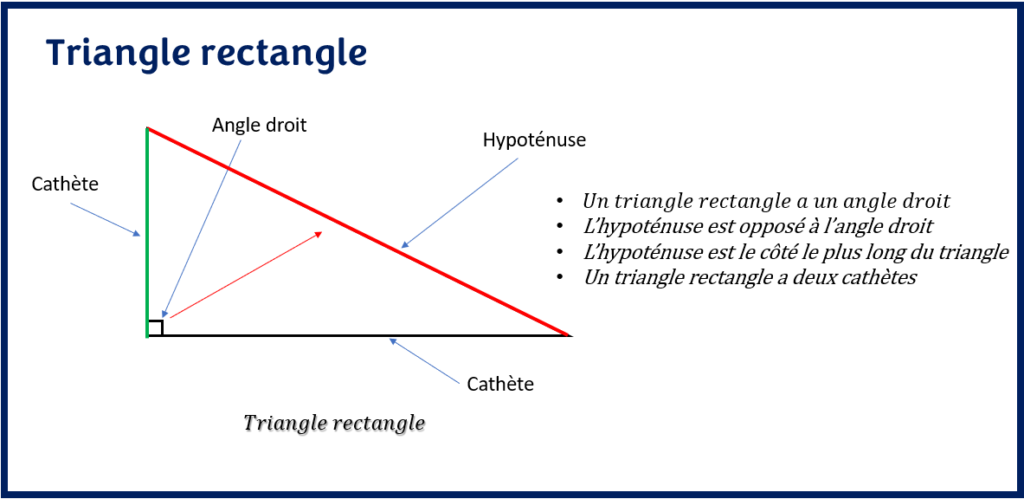
Un triangle rectangle est une figure géométrique à trois côtés. Plus précisément, dans un triangle rectangle, il y’a toujours un côté qui est plus long que les deux autres côtés. En effet, on l’appelle l’hypoténuse.
Par conséquent, un triangle rectangle possède toujours un angle droit. En théorie, un angle droit est tout angle de 90 degrés.
L’hypoténuse dans un triangle rectangle est toujours le côté opposé à l’angle droit. Les autres côtés sont appelés les cathètes. En ce sens, un triangle rectangle a deux cathètes et une hypoténuse.
Un triangle rectangle isocèle est un triangle rectangle qui a ses deux cathètes égales.
Théorème de Pythagore
Le théorème de Pythagore est une relation mathématique qui s’applique uniquement dans les triangles rectangles.
Pour ainsi dire, s’il n’y a pas un angle droit dans un triangle, le théorème de Pythagore ne s’applique pas.
Le théorème de Pythagore ou la relation de Pythagore s’énonce comme suite :
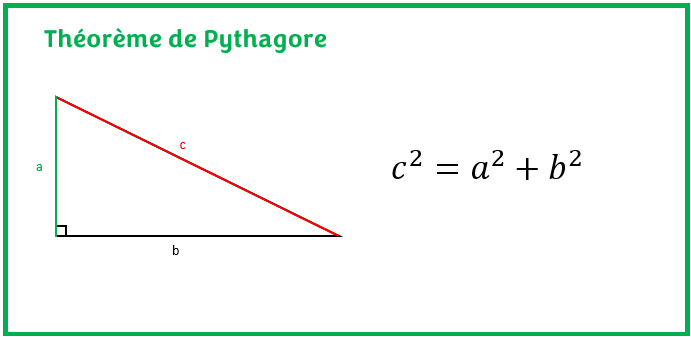
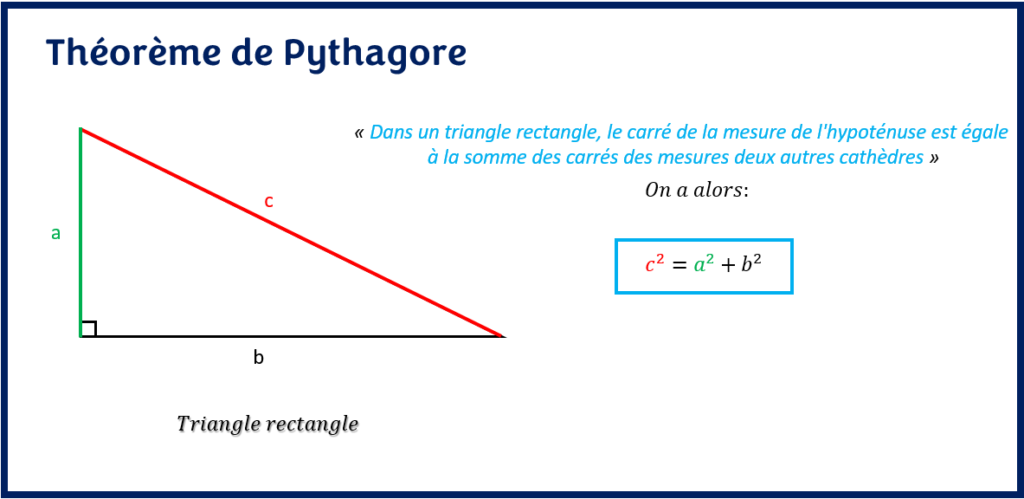
« Dans un triangle rectangle, le carré de la longueur de l’hypoténuse est égal à la somme des carrés des deux autres cathètes »
On nomme souvent par c la mesure de l’hypoténuse, par a, la mesure d’une cathète et par b, la mesure de l’autre cathète.
Compte tenu de cette notation, le théorème ou relation de Pythagore devient:
c2 = a2 + b2
En règle générale, il faut connaitre au moins la mesure de deux côtés du triangle pour déterminer la mesure du dernier côté restant.
Application du théorème de Pythagore
Considérons par exemple deux exemples, principalement pour illustrer le théorème ou relation de Pythagore.
Calculer l’hypoténuse d’un triangle rectangle
Exercice 1
Soit un triangle rectangle ABC rectangle en B dont AB=4 cm et BC=3 cm.
Que vaut la mesure de AC ?

Dans ce cas, puisqu’on connait les mesures de deux côtés du triangle, on peut déterminer la mesure du dernier côté. À cet égard, le côté AC correspond à l’hypoténuse du triangle rectangle.
Trouver la mesure d’une cathète dans un triangle rectangle
Exercice 2
Soit un triangle rectangle ABC rectangle en B dont AB=6 cm et AC=10 cm.
Que vaut la mesure de BC ?
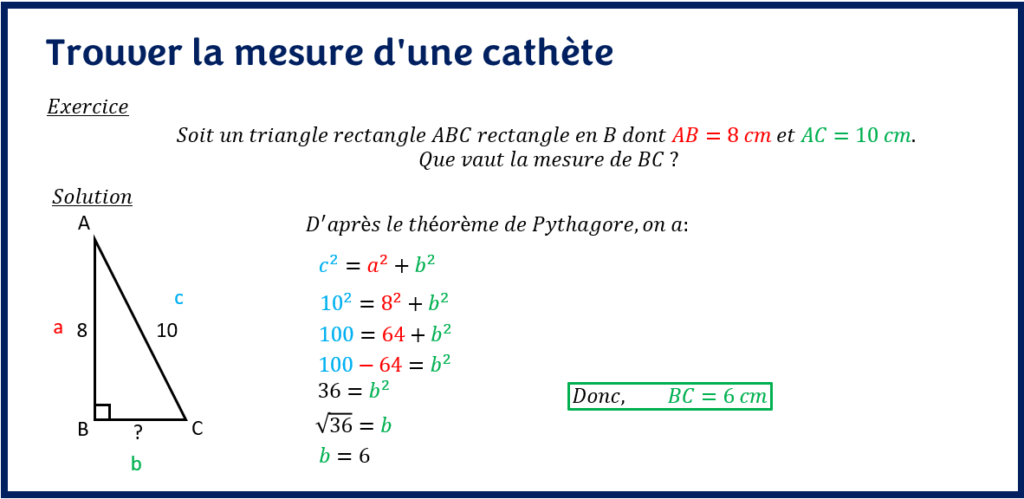
Dans les grandes lignes, puisqu’on connait les mesures de deux côtés du triangle, on peut déterminer la mesure du dernier côté. Ainsi, le côté BC correspond à l’une des cathètes du triangle rectangle.
Conseils et astuces sur le théorème de Pythagore
- Le théorème de Pythagore s’applique uniquement dans un triangle rectangle
- Un triangle rectangle est un triangle possédant un angle à 90 degrés
- L’hypoténuse dans un triangle rectangle est opposée à l’angle droit
- L’hypoténuse est le côté le plus long d’un triangle rectangle
- Un triangle rectangle isocèle est un triangle dont les deux cathètes ont la même longueur
- L’hypoténuse dans un triangle rectangle peut être directement calculée avec la formule: c = √( a2 + b2 )
- La mesure d’une cathète peut directement être calculée avec la formule: a=√(c2 – b2 ) ou b=√(c2 – a2 )
- La relation de Pythagore ainsi que les relations métriques permettent de calculer des mesures manquantes dans un triangle rectangle
FAQ sur le théorème de Pythagore dans un triangle rectangle
En fait, dans un triangle rectangle, le carré de la mesure de l’hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés. On a donc: c2 = a2 + b2
avec :
c : Hypoténuse du triangle rectangle
a : Cathète du triangle
b: Cathète du triangle rectangle.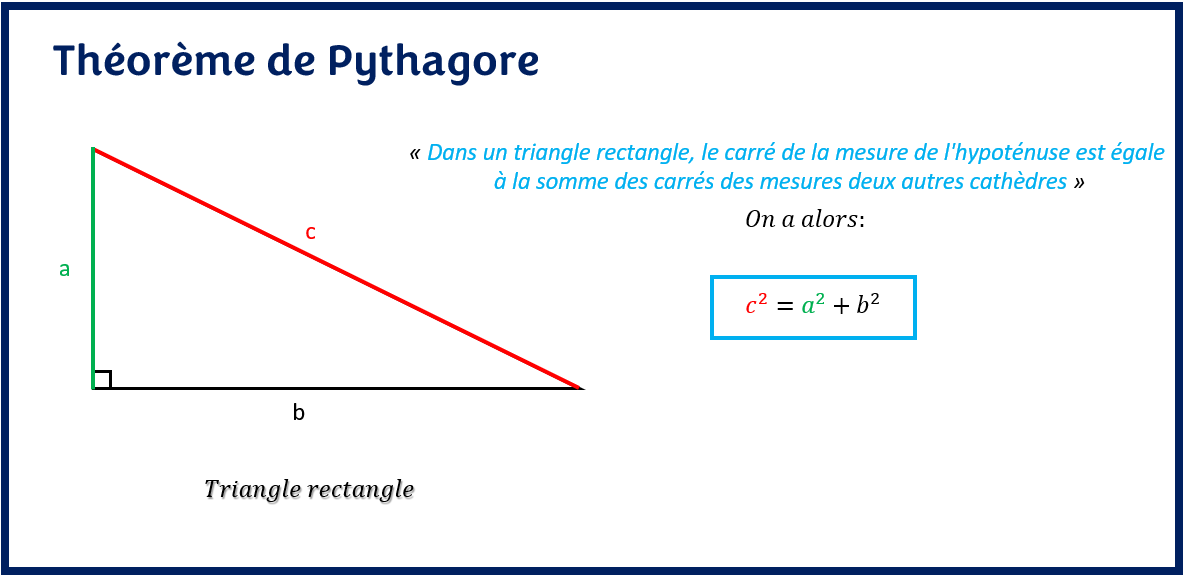
En général, le théorème de Pythagore ou relation de Pythagore peut se décomposer en 5 étapes simples:
1. Vérifier si on a un triangle rectangle : présence d’un angle de 90 degrés
2. Identifier l’hypoténuse du triangle rectangle: c’est le côté opposé à l’angle droit
3. Vérifier que l’on a deux longueurs de côtés du triangle connus
4. Appliquer la formule du théorème de Pythagore: (Hypoténuse)2= (premier côté du triangle)2 + (deuxième côté du triangle)2
5. Remplacer les longueurs connues dans la formule et isoler la donnée manquante.
Le théorème de Pythagore s’utilise uniquement dans un triangle rectangle si on connait au moins deux longueurs des côtés du triangle. En effet, pour résoudre un exercice nécessitant la relation de Pythagore, l’on peut suivre les cinq étapes suivantes:
1. Vérifier qu’on a un triangle rectangle : présence d’un angle de 90 degrés
2. Identifier l’hypoténuse du triangle rectangle: c’est le côté opposé à l’angle droit
3. Vérifier que l’on a deux longueurs de côtés du triangle connus
4. Appliquer la formule du théorème de Pythagore: (Hypoténuse)2= (premier côté du triangle)2 + (deuxième côté du triangle)2
5. Remplacer les longueurs connues dans la formule et isoler la donnée manquante.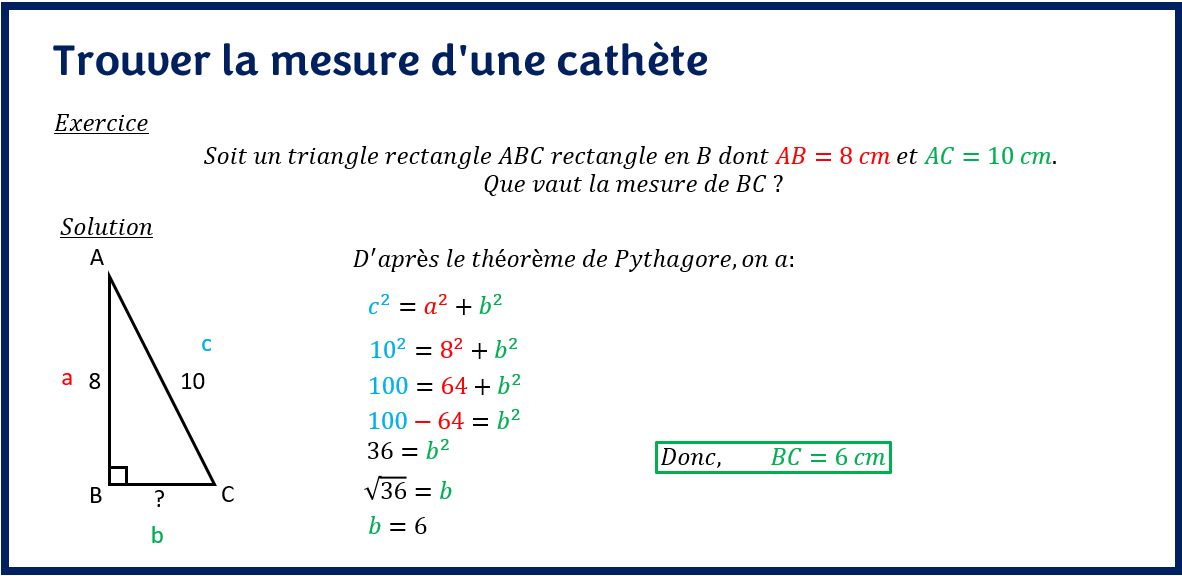
En bref, la réciproque de Pythagore est utilisée pour démontrer si triangle est un triangle rectangle. Elle s’énonce comme suite:
<< si dans un triangle, le carré de la longueur du plus grand côté est égal à la somme des carrés des longueurs des deux autres côtés, alors ce triangle est rectangle >>.
Dès que le triangle est rectangle, le plus long côté est appelé hypoténuse du triangle rectangle.
En principe, le théorème de Pythagore permet de calculer une mesure manquante dans un triangle rectangle.
En d’autres termes la relation de Pythagore sert à calculer la longueur de la diagonale d’un carré ou d’un rectangle. Cela dit il sert à calculer l’apothème d’un polygone : le pentagone, l’hexagone, l’heptagone, l’octogone, etc.
Il sert aussi à calculer l’apothème d’un cône ou la hauteur d’une pyramide.
En général, on essaye d’isoler un triangle rectangle ayant deux longueurs connues et on utilise la relation de Pythagore pour déterminer le denier coté manquant.
En fait, pour démontrer la réciproque de Pythagore, on suit les étapes suivantes:
– Calculer le carré de chacune des trois longueurs du triangle
– Calculer la somme des deux plus petits résultats obtenus de l’étape 1
– Vérifier si cette somme obtenue à l’étape 2 est égale à la valeur du carré du côté le plus long obtenu à l’étape 1
– Le triangle est rectangle si l’étape 3 est vraie.
Ces étapes peuvent en résumé se concentrer en une seule question: est-ce que le carré de la longueur du plus long côté est égal à la somme des carrés des longueurs des deux autres côtés?
Sujets similaires
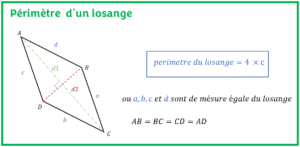
- Périmètre d’un losangeL’objectif est d’apprendre à calculer le périmètre d’un losange et de connaitre ses propriétés avec des exemples résolus.
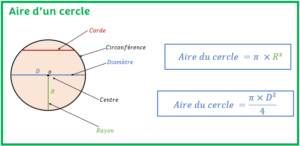
- Aire d’un cercleL’objectif est d’apprendre comment calculer l’aire d’un cercle et de connaitre ses propriétés avec des exemples résolus.
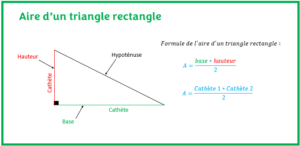
- Aire d’un triangle rectangleL’objectif est d’apprendre comment calculer l’aire d’un triangle rectangle de plusieurs façons différentes avec des exercices résolus.
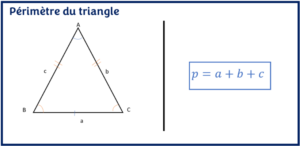
- Périmètre du triangleL’objectif est d’apprendre à calculer le périmètre du triangle et de connaître ses propriétés à partir d’exercices résolus.
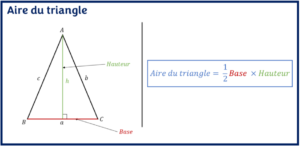
- Aire du triangleL’objectif est d’apprendre à calculer l’aire d’un triangle et de connaître ses propriétés à partir d’exercices résolus.
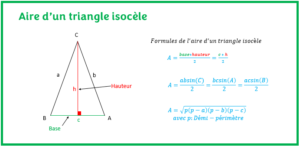
- Aire d’un triangle isocèleL’objectif est d’apprendre à calculer l’aire d’un triangle isocèle de plusieurs façons différentes avec des exercices résolus.
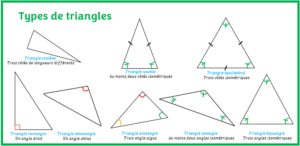
- Les types de trianglesL’objectif est d’apprendre les différents types de triangles existants et leurs propriétés avec des exemples résolus.
- Périmètre du rectangleL’objectif est d’apprendre à calculer le périmètre du rectangle et de connaître ses propriétés à partir d’exercices résolus.