Périmètre du rectangle

L’objectif est d’apprendre à calculer le périmètre du rectangle et de connaître ses propriétés à partir d’exercices résolus.

Sommaire

Rappel et mise en contexte

Un rectangle est un quadrilatère à quatre côtés deux à deux égaux et parallèles avec quatre angles droits. Un quadrilatère est une figure géométrique qui a quatre côtés. On peut citer par exemple, le carré, le rectangle, le parallélogramme, le losange, le trapèze, etc.

Un rectangle a une longueur et une largeur. Le plus long côté du rectangle s’appelle la longueur et le côté le plus court est appelé la largeur. Le rectangle a donc deux longueurs et deux largeurs.

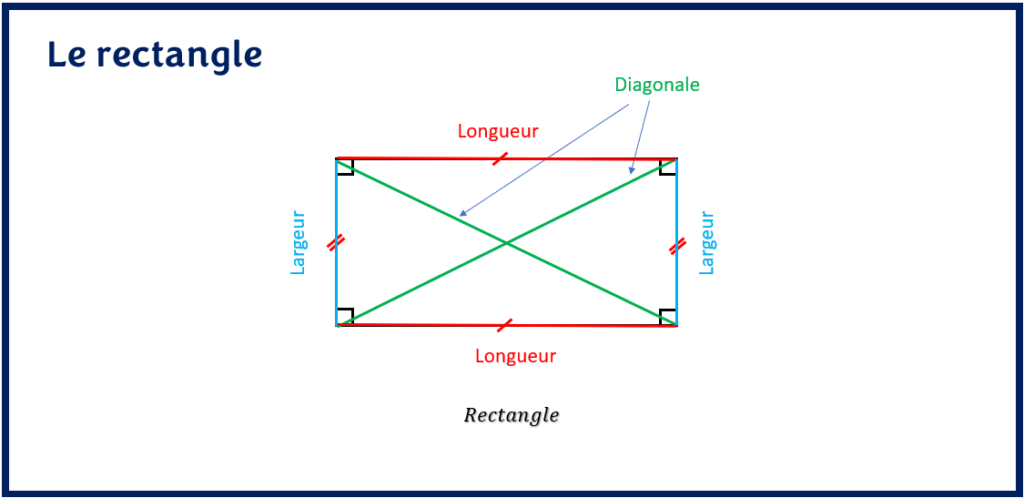
Le rectangle a deux diagonales de même longueur. Les diagonales du rectangle se coupent au centre du rectangle. Une diagonale est le segment de droite qui relie deux sommets opposés du rectangle. La diagonale du rectangle peut se calculer avec le théorème de Pythagore si l’on connaît sa longueur et sa largeur.

Dans cet article, nous allons apprendre à calculer le périmètre du rectangle. Il est la suite de l’article de l’aire du rectangle.

Formule périmètre du rectangle

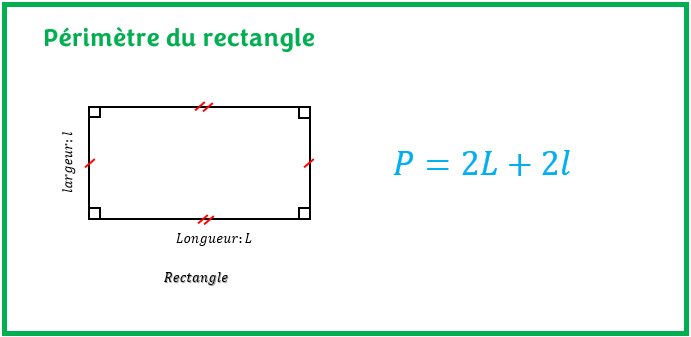
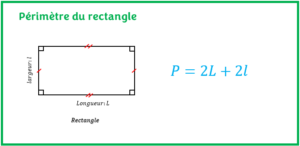
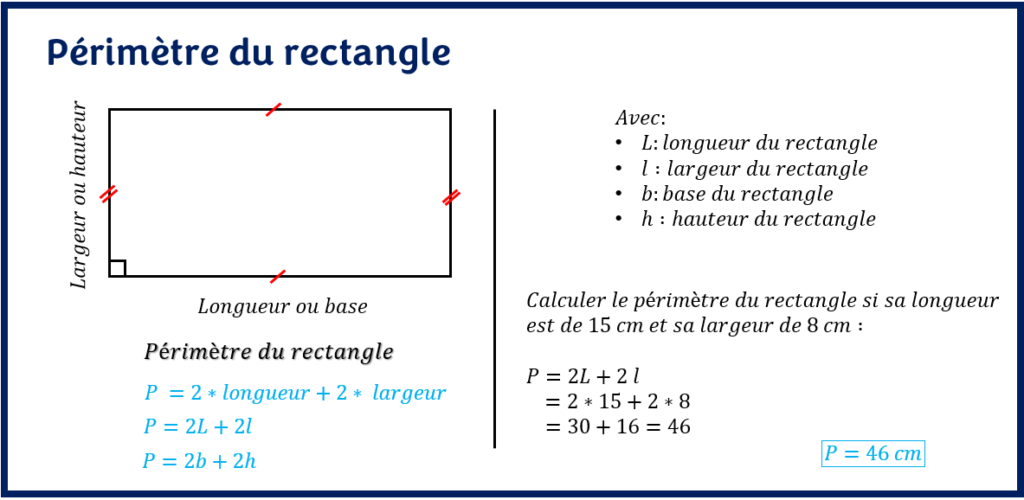
Le périmètre du rectangle est la somme de tous les côtés du rectangle. Il est donc une mesure de la longueur des contours du rectangle. Puisque le rectangle a deux longueurs et deux largeurs, le périmètre du rectangle se calcule par la formule suivante:

P = 2 * la mesure de la longueur + 2 * la mesure de la largeur

P = 2*L + 2*l

Avec, L: mesure de la longueur du rectangle et l : mesure de largueur du rectangle

Dans certaines situations, la longueur du rectangle peut être considérée comme la base du rectangle et la largeur comme la hauteur du rectangle et vise versa. Tout dépend du dessin du rectangle.

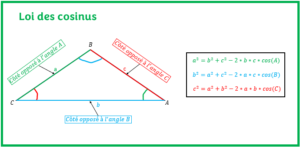
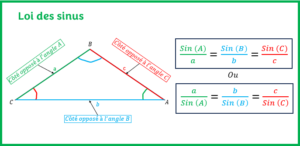
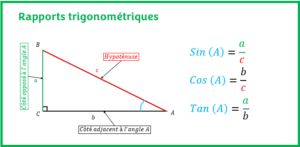
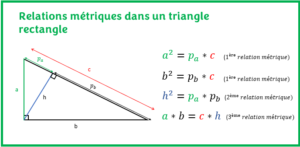
Le calcul du périmètre du rectangle est assez simple si l’on connaît les mesures de ses côtés. Seulement, dans nos nombreux problèmes de calcul de périmètre, il est nécessaire de calculer soi-même la mesure de la longueur ou de la largeur du rectangle avant de calculer son périmètre. Pour ce faire, vous disposez de plusieurs outils pour calculer ces mesures manquantes entre autres la relation de Pythagore, le théorème de Thalès, les rapports trigonométriques (SOH-CAH-TOA ou CAH-SOH-TOA), les relations métriques, la loi des sinus et la loi cosinus pour ne citer que cela.

Le périmètre d’une figure est une mesure de la longueur des contours de la figure.

L’unité du périmètre est le mètre (m). De façon plus générale, c’est une unité de longueur (les multiples du mètre) : km, hm, dam, dm, cm, mm

Propriétés d’un rectangle

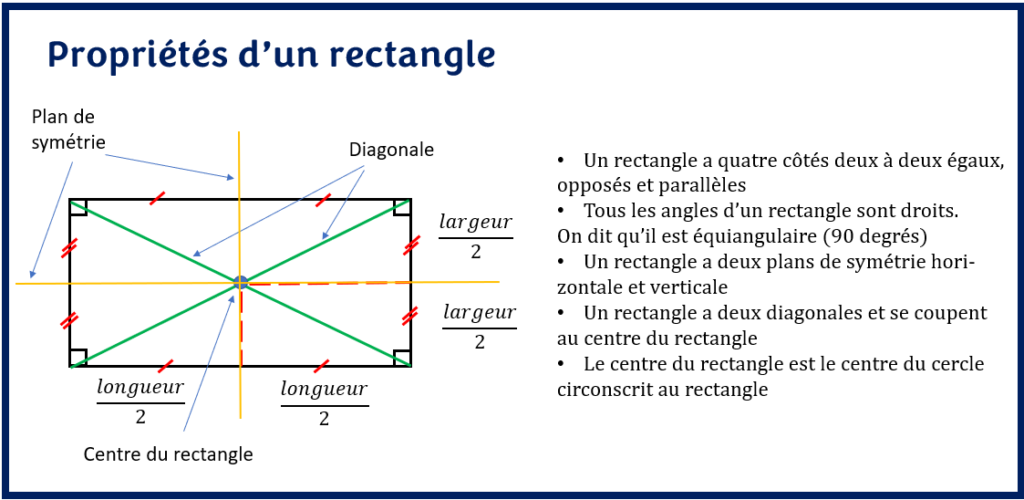
• Un rectangle a quatre côtés deux à deux égaux, opposés et parallèles
• Le rectangle a deux longueurs et deux largeurs
• Un rectangle a deux diagonales de même longueur qui se coupent au centre du rectangle
• Tous les angles d’un rectangle sont droits. On dit que le rectangle est équiangulaire.
• Un rectangle a deux plans de symétrie de réflexion horizontale et verticale partageant la longueur et la largeur en deux parties égales
• La longueur de la diagonale du rectangle peut être obtenue par le théorème de Pythagore.
• Le centre du rectangle (point de rencontre des diagonales) est le centre du cercle circonscrit au rectangle.

Conseils et astuces concernant le périmètre du rectangle

• Attention à la conversion d’unité lors du calcul du périmètre du rectangle. La longueur et la largeur doivent avoir la même unité.
• Le rectangle et le carré sont des quadrilatères
• La longueur ou la largeur du rectangle peuvent se calculer en utilisant son périmètre ou son aire s’ils sont connus.
• Le plus long côté du rectangle est appelé longueur et le côté le plus court est sa largeur
• Consulter la vidéo explicative ou demander l’assistance d’un tuteur au besoin

Vidéo explicative sur le périmètre du rectangle

Vous pouvez consulter cette vidéo sur le périmètre du rectangle

Si vous n’avez toujours pas compris, vous pouvez consulter les la foire aux questions.

FAQ sur le périmètre du rectangle

Sujets similaires

• 
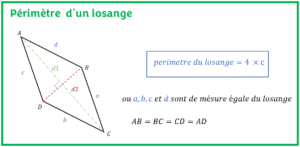
  Périmètre d’un losange
  L’objectif est d’apprendre à calculer le périmètre d’un losange et de connaitre ses propriétés avec des exemples résolus.
• 
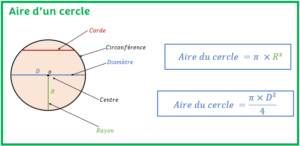
  Aire d’un cercle
  L’objectif est d’apprendre comment calculer l’aire d’un cercle et de connaitre ses propriétés avec des exemples résolus.
• 
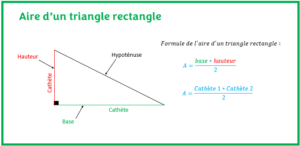
  Aire d’un triangle rectangle
  L’objectif est d’apprendre comment calculer l’aire d’un triangle rectangle de plusieurs façons différentes avec des exercices résolus.
• 
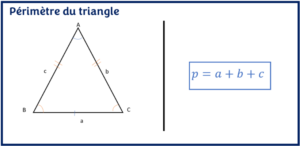
  Périmètre du triangle
  L’objectif est d’apprendre à calculer le périmètre du triangle et de connaître ses propriétés à partir d’exercices résolus.
• 
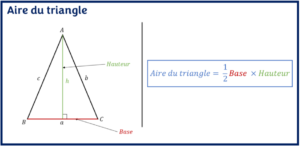
  Aire du triangle
  L’objectif est d’apprendre à calculer l’aire d’un triangle et de connaître ses propriétés à partir d’exercices résolus.
• 
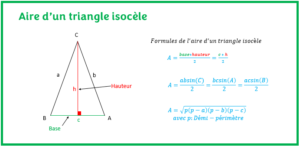
  Aire d’un triangle isocèle
  L’objectif est d’apprendre à calculer l’aire d’un triangle isocèle de plusieurs façons différentes avec des exercices résolus.
• 
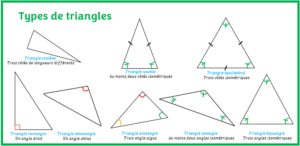
  Les types de triangles
  L’objectif est d’apprendre les différents types de triangles existants et leurs propriétés avec des exemples résolus.
• 
  Périmètre du rectangle
  L’objectif est d’apprendre à calculer le périmètre du rectangle et de connaître ses propriétés à partir d’exercices résolus.
• 
  LOI DES COSINUS
  L’objectif est d’apprendre à utiliser la loi des cosinus dans un triangle afin de déterminer une mesure manquante d’un côté ou d’un angle dans un triangle quelconque.
• 
  LOI DES SINUS
  L’objectif est d’apprendre à utiliser la loi des sinus dans un triangle afin de déterminer une mesure manquante dans un triangle quelconque.
• 
  RAPPORTS TRIGONOMÉTRIQUES
  L’objectif ici est d’apprendre à utiliser les rapports trigonométriques pour calculer une mesure manquante ou un angle manquant dans un triangle rectangle avec des exemples résolus.
• 
  RELATIONS MÉTRIQUES DANS UN TRIANGLE RECTANGLE
  L’objectif est d’apprendre à utiliser les relations métriques dans un triangle rectangle pour déterminer une mesure manquante à partir d’exercices résolus.